井出治氏の超効率インバーター「デゴイチ」にかかる第３起電力のエネルギー源についての考察から、見いだした「 発散トーラス 」
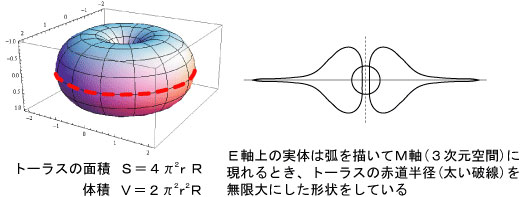
図１
右について、その考えられる性質について解説します。理解を深めるために前提が長いです。
手元資料によれば２０１２年５月頃には気付いていました。 上記考察は、計算を用いず何十枚かの幾何図形によってＭ軸（３次元物理空間）＋Ｅ軸（真のエネルギー）の４次元空間を頭の中に描くことで進めました。
この考察の概略を以下に示します。
- 電気と磁気の現象は、常に直交して現れる。
- 仮説、『電気磁気現象は、一つの（何か：以下、実体と呼ぶ。）が電場・磁場の異なる現象として現れる。』
- 一つの実体を別の次元軸上（以下、Ｅ軸と呼ぶ。）に存在するものと仮定し、Ｅ軸－Ｍ軸平面の間での相互のやりとり（Ｅ－Ｍ軸平面での位相変化）により第３起電力が現れると考える。
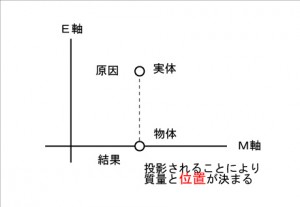図２ - Ｅ－Ｍ軸平面において、上記３．の操作を「積分を伴う回転投影」と呼ぶ。
- 井出氏のトランスに与えられる急峻なパルスを電子の運動にかかる時間の次数として捉える。ただし、Ｅ軸上の実体がＭ軸に投影される回数は、当該次数に１を加えたものになる。
- 観測者に対してトランス内にある電子が静止の状態を次数”０”、速度を次数”１”、加速度を次数”２”、躍度を次数”３”と考える。
- 電子の次数によって、Ｅ－Ｍ軸平面での位相が反時計方向に９０度ずつ変化（回転）する。
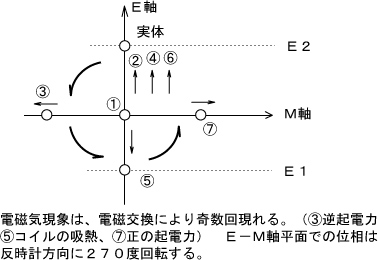図３ 次数”０”→投影の回数は① 次数”１”→回数③ 次数”２”→回数⑤ 次数”３”→回数⑦ である。 - 位相の変化によって、Ｍ軸上に電場と磁場として現れる。
- 物質は、加速しても光の速度には到達しない。
- ところが、電子に躍度を持たせることによりＭ軸との位相がゼロになる。（弧理論の考え方による光の速度に相当する。）
- 位相ゼロのとき、Ｅ軸上の実体は、Ｍ軸上に現れる。
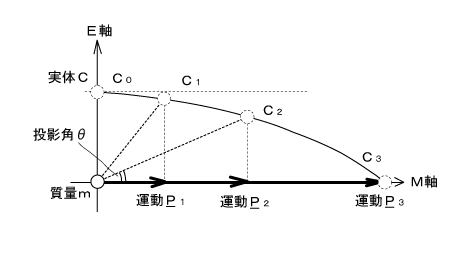図４ 運動Ｐ３の状態が現れる - このとき実体は、Ｅ－Ｍ軸平面に弧（Ark）を描く。
- 弧のＭ軸との接点であるＰ３の３次元形状が発散トーラスである。
- 弧は、Ｃ３からＣ２、Ｃ１を経て次数”０”であるＣ０の状態（静止状態）に戻ろうとするが、このとき電子を正の方向へ加速しようとする。これが第３起電力のことである。（※最短距離で90度の位置へ戻ろうとするということ。図３の⑦→⑤→③→①の様に、時計方向には戻らない。）
- 仮説による投影のたびに積分を繰り返すことにより、「距離の７乗に逆比例する力」を持つ。
因みに、躍度（jerk）とは、単位時間当たりの加速度の変化のことです。 １２．の思考へ到達したときの図が
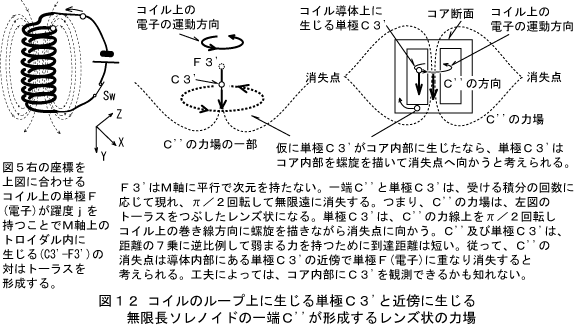図５
でした。 図５で大事なのは、与えたパルスのコイルに対する向きによって、 発散トーラス は、上下半分だけ生じるということです。 発散トーラス 全体が生じることはありません。（たぶん例外があると思いますけれども、それは別途です。）
頭の中で４次元空間のことを思考していますのでとても複雑です。
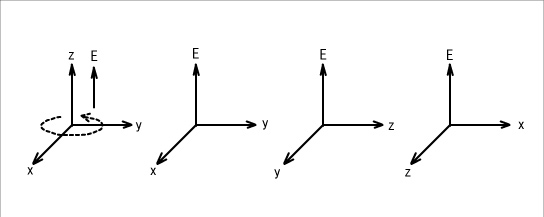図６
の様に、Ｅ－Ｍ軸平面は４つの３次元空間に分解できます。 Ｅ軸上の実体がｘｙｚ空間との間で位相を変化させながら投影を繰り返すのですから、最終的に次数”３”のときに３次元空間に発散トーラスを描くだろうと理解することは、ほとんど不可能かと思います。
図１右を元に作成したのが 発散トーラス の３ＤＣＧモデル
.
です。 因みに、「電磁気現象が別の次元軸上にある（何か）が原因である」というアイディアは管理人によるものではありません。 しかし、このアイディアの（何か）が
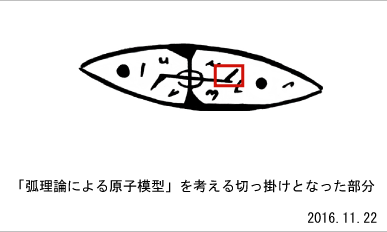図７
の赤枠で囲ったヒゲの部分ではないかと考えたのは、たぶん１９８０年代頃だったと思います。 そして、この考察に没頭していた２０１２年の頃には、まだ岡潔の言葉を知りませんでした。 この頃は、まだ時間は存在すると考えていましたので、パルスを扱うに時間の次数という考えを用いました。 ですから、弧電磁気論や冒頭の考察を書いていたころまで、自然宇宙のことを時間軸＋３次元物理空間＋Ｅ軸の計５次元だという認識でいました。ただ、足跡
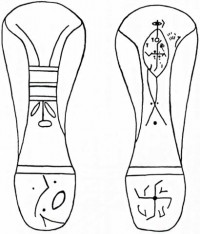図８
の解析から、「時間」の取り扱いが何か変であることは気付いていました。（※時間の表記はあるものの付け足しにしか過ぎない。）
さて、前置きが長くなりました。
電子は、質量と電荷を持っています。電荷は電気力線を発しています。
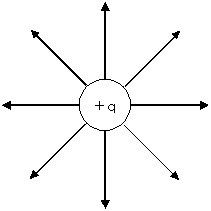図９ 発散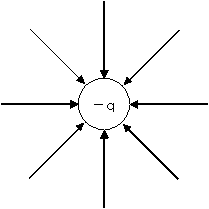 
図１０ 収束
出典：電気力線と電束
そして、観測者に対して運動する電子は磁場を持ちます。
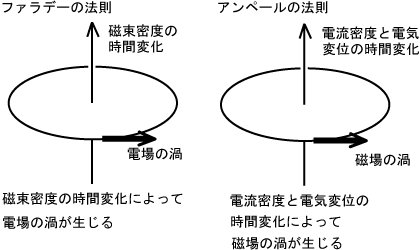図１１右 参考
単極である電子の特徴を以下にまとめます。
- 単極である。
- 質量を持つ。
- 電荷を持ち、電気力線を持つ。発散、または収束。
- 渦なし。
- 距離の二乗に逆比例する力
運動する電子の周囲にできる磁場は双極です。必ず２つの極ができるトーラス
図１ （再掲）
左の形状をしています。 磁場の特徴を以下にまとめます。
- 双極である。
- 質量を持たない。
- 磁力線（磁束）を持つ。
- 渦あり。
- 距離の二乗に逆比例する力（距離の三乗の場合もある）
ここで、発散トーラスの性質です。単極と双極の２つの性質を併せ持っています。
- 双極であるが上下半分しか生じない。従って単極の性質を持っている。
- 質量を持たない。
- 発散あり。
- 渦あり。
- 距離の７条に逆比例する力
こうしてみると、発散トーラスは、単極のように物質間を伝搬するが質量を持たない。 しかも到達距離は短いが非常に強い力の場であろうとわかります。 これが２０１４年６月に提唱した弧の力場です。
最近の考察では、
- 電子が持つ弧の力場は、もう一つあるようです。（プラスとマイナスの計２）
- 殻電子には常に躍度が働いているようです。これまでに何度か書いてきた「電子が描く弧は、静止しようとするが故に回転を加速する」ということが起きているようです。
- 「回す」と「回る」の違いについて、一見同じに見えるが、「回る」には２つ以上の力が働いている。引力と斥力が同時に働いている。
- 躍度を持たせるには、次数”２”の加速度を基本とし、かつ「回る」を用いる必要がある。
- 単極誘導モーターは、回転運動であるから次数”２”である。
- これに、次数を”１”加えることができれば躍度を持つ装置が実現できるはず。
- ただし、人類の作る装置に躍度を積極的に利用したものはない。
最も近いのが
.
動画１
もしくは
.
動画２
です。 仮に動画に出てくる機械装置に躍度が出ていたとしても一瞬であるはずです。しかも、機械や身体に強い負荷がかかります。
回転運動には次数２の加速度があります。 工夫次第で次数３の躍度を出せるのではないか？と考えます。 歳差運動を強制させることで実現できるかも知れませんが、今のところ具体的な方法はわかりません。
ところで、
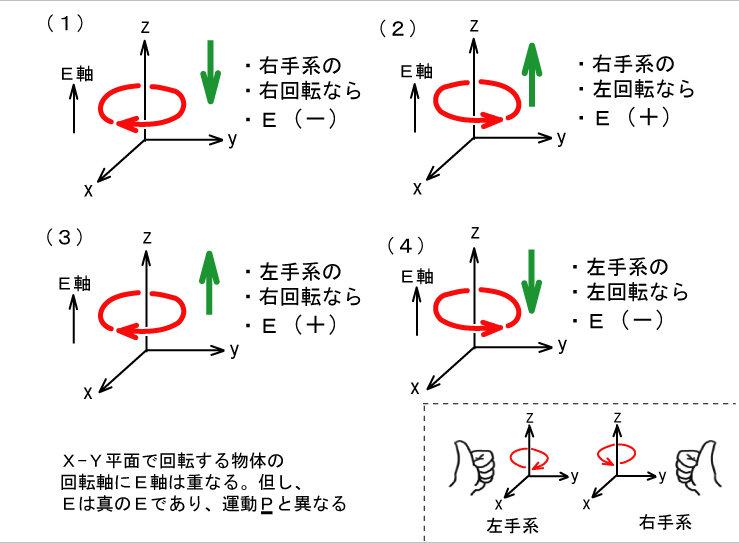図１２
は、２０１６年９月５日エネルギー軸制御の可能性という記事に出した図なのですけれど、発散トーラスを上図に当てはめますと
- 右手系の右回転ならば、親指の向きはＺ軸の（－）方向に
- 右手系の左回転ならば、親指の向きはＺ軸の（＋）方向に
- 左手系の右回転ならば、親指の向きはＺ軸の（＋）方向に
- 左手系の左回転ならば、親指の向きはＺ軸の（－）方向に
なります。つまり、発散トーラスには４つの状態がありそうだということです。
ここで、図６によりｘｙ平面内で回転する物体の回転軸（Ｚ軸）方向にＥ軸は重なりますので１．～４．は、そのままＥ軸方向の向きになります。これが発散トーラスの３次元物理空間とＥ軸との関係です。 つまり、このような装置が実現できれば、装置の観測者に対する真のエネルギー値を制御できるはずだということです。 ただし、２．と４．は発散ですけれど、１．と３．は収束になるのでは？と考えます。 今のところ「無限遠からの収束」というのが頭でイメージできません。
また、上記の発散トーラスの性質は、
写真１ 出典：“Cold Electricity” demo with light bulb in water
ＥＭＡモーターで云われた「冷たい電流」に似ています。質量を持たないならば、感電しにくいかも知れません。磁気的な何かが流れるのですから、まるで磁気単極です。 まさに電気磁気の融合（Electro-Magnetic Association）です。
図１２を何の切っ掛けで思いついたのか、まったく覚えていません。なかなか面白い図です。 それにしても超弦理論とかＭ理論で云われる１０次元とか１１次元とかは、次元軸の数が足りないから指折り足しただけのように思えます。余分な次元軸とＭ軸（３次元空間）とのやりとりを考えたことはないはずです。そんなの不可能です。思考の行き止まりです。 数学を用い、複雑で抽象的な概念を扱うことが高等高尚なことだと考えられているようですけれど、それは間違いです。それだと先に進めなくなります。 当たり前、簡単、具体的なことにこそ、物や事の本質があるように思います。 五感でわからないものは「ない」としか思えない人たちが一線を越えてから、「五感でわかる」ことを蔑ろにしています。 五感でわかるもの以外の中に何か本当のことが在るかも知れないと考えた結果、「五感でわかる」ことを大事にするというのは皮肉なことです。
Follow me!
