これまで、数学者岡潔の「時間」について語った言葉を起点に考察を続けてきました。岡潔【２】自然科学者の時間空間）より引用します。
時間というものを表わそうと思うと、人は何時も運動を使います。で、直接わかるものではない。運動は時間に比例して起こると決めてかかって、そういう時間というものがあると決めてかかって、そして、時間というものはわかると思っています。
人は時間の中なんかに住んでやしない。時の中に住んでいる。
時には現在、過去、未来があります。各々、全く性質が違うんです。それ以外、いろいろありますが、時について一番深く考えたのは道元禅師です。
が、その時の属性のうちに、時の過去のうちには「時は過ぎ行く」という属性がある。その一つの性質を取り出して、そうして観念化したものが時間です。
（１）考察を続けた結果、管理人は
時間とは過ぎ行く運動の記憶（記録）である。
と結論づけました。
（２）時間は運動を元に作られます。 時計は
機械装置の運動を回転に変えて盤の中心の針を動かします。盤面を区切り、数字を割り当てます。針の位置（角度）を数に置き換えたのが時間です。
今、この時計の運動を直線に置き換えます。
図１
のように、短針を直線に合わせます。時間の経過とともに文字盤は右から左方向へ転がります。こうして、１～１２の数を附した数直線が得られます。 この数直線はおよそ３６時間（１日半）を表しています。
ここで図１の（左右を反転した上で）縮尺を極端に大きくして、起きた出来事を書込ことにより
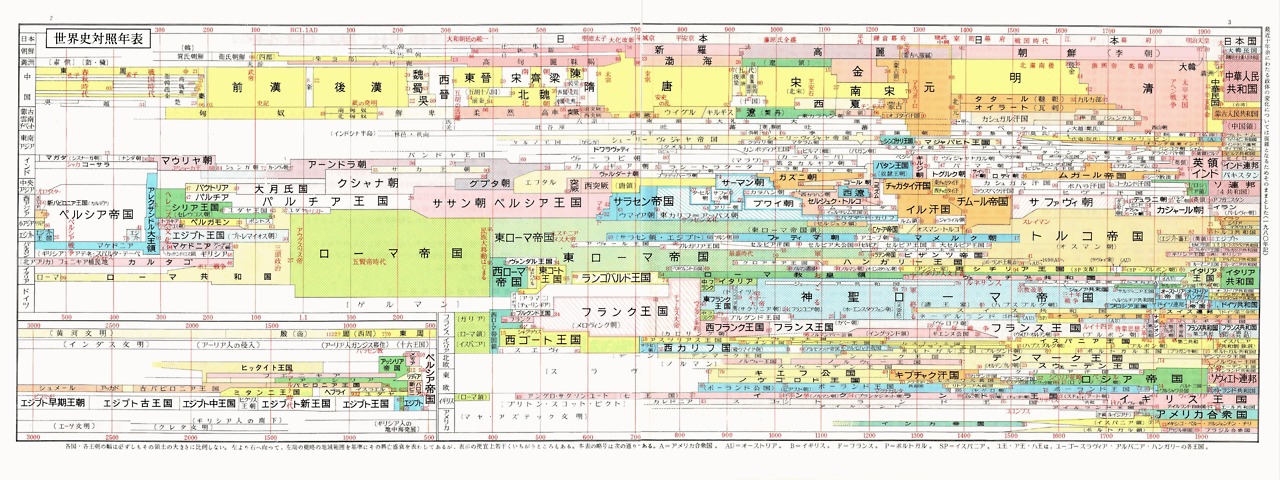図２ 出典：輝き始めた日本より世界史対照年表表
を得ることができます。 ご存知の通り、この歴史年表は西暦０年を基準にしたものです。
時計の運動からから得た歴史年表を観てわかるように、冒頭の考察（１）「時間とは過ぎ行く運動の記憶（記録）」というのは図２の歴史年表と本質は同じであることがわかります。
本題です。ここに１本の色鉛筆があります。
写真１
鉛筆の左端の位置を（A）、右端の位置を（B）とします。位置と位置の隔たりを距離または長さといいます。これに基準となる定規（モノサシ）をあてます。単位はミリメートルです。 （A）が５０で（B）がだいたい２２２を示しています。差し引き色鉛筆の長さは１７２ミリメートルです。
定規を取り除きます。
写真２
そして、色鉛筆を除きます。
写真３
位置（A）と（B）が意味を持つのは量としての色鉛筆（被測定物）と定規（測定基準）があったからです。 岡潔が言った「数は量のかげ」ということの意味がここにあります。
ここで、写真３と図１を比較します。 位置（A）（B）に数を附すことができるのは、定規があったからです。 同様に時計から位置を示す数直線が得られたのは、時計という機械装置の運動が位置を持つからです。 しかし、時計の場合、位置に対応する「量」は存在しません。色鉛筆やモノサシが無いのと同じです。
図１の場合、モノサシが時計の運動です。運動そのものではありません。運動を位置に置き換えたものです。対応する量がありません。ですから、時間に対する単位「年月日時分秒」をつけることは不適切です。時間を基本物理量として使うことに同意できません。
岡潔が述べたように時計という機械装置の運動が位置に附した「数」（つまり時間）に比例して起きるかどうかわかりません。 何故なら、過ぎ行く運動の記憶ですから、
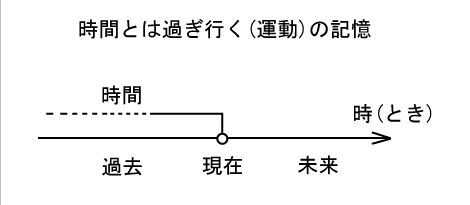
図３
時間を時（とき）の現在と時（とき）の未来に適用できるかどうかわからないのです。計測により得た結果は既に過去です。 「運動が時間に比例して起きるかどうか」の意味はここにあります。
こうして時計という手元にある機械装置を元にして作られた時間は、
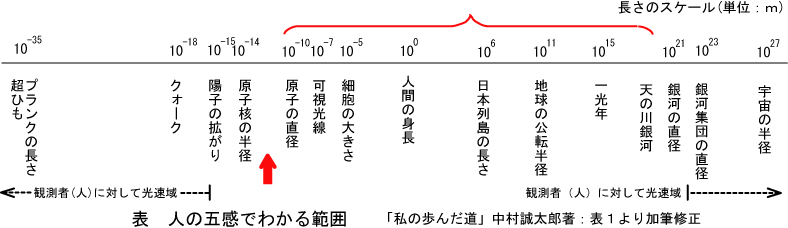表１
赤い括弧の内側に適用できることは確かです。 被測定物が光の速度（運動）に近い場合（図４の両端）は、疑問であると管理人は考えます。 表１の両端は、手元の時計（モノサシ）を使って光速で運動する色鉛筆を測定することに相当します。
誰もが知っていることとして、位置と運動は相対的です。それ故、運動から作られた時間も相対的であってしかるべきです。ですから歴史年表は、西暦０年を基準にしているのです。どこに基準を置いてもよい。 ビッグバンが本当なら魚の鱗や木の年輪のような宇宙絶対時を示す痕跡があるはずです。その痕跡を探すべきと過去に書きました。
上記について、第３者に説得力があるかどうかよくわかりません。 天才である岡潔は、熟考の末に結晶化した結論のみを簡単な言葉でサラリと述べて終わります。これが凡人である管理人にはわからないのです。本当に大変です。
Follow me!
