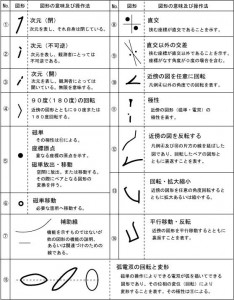
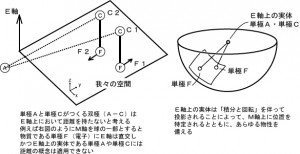
これまでの考察の結果、原子の構造を理解することは即、宇宙の構造を理解することにつながるということがわかってきました。 考察の過程に於いて、拙著弧電磁気論も随時変更しなければなりません。弧電磁気論の宇宙論ｐ５５に示した凡例は
図１でした。
弧理論（旧弧電磁気論）では２つの直線が交わるとき直交であるならば凡例⑧のように●印を用います。
図２
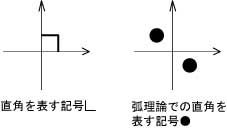
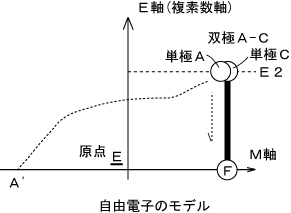
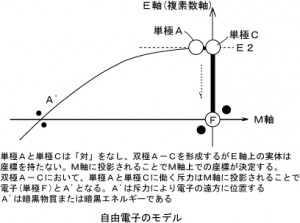
数学では直角を表すとき左のように書きますし、弧理論では右図のように書きます。 一方、凡例⑨では、直交以外の交差は小さな●印を用いて表すとしましたけれど、過去記事、「量子もつれ」の現象から考える「Ｅ軸の性質」に示したように、Ｅ軸上の実体はＭ軸に「回転と積分」を伴って投影されることで初めて座標を持つと定義しました。すると自由電子のモデルは
図３
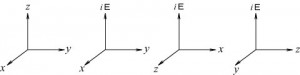
のように示されることになります。図３のＡ’はＭ軸に直交しているのにも関わらず、見た目の角度は直交になっていません。そこで、図１の凡例⑨を
図４
右図のように変更します。
図５
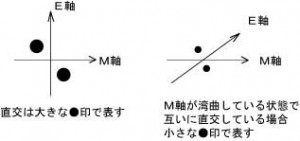
右図のように、Ｅ軸上の実体は投影されるまでＭ軸上において座標を持たないと考えねば「量子もつれ」の現象は説明できませんでした。 ですから、Ｅ軸上の実体から見たＭ軸は湾曲しているように見えます。 すると図３の自由電子モデルを図４の右に示す書き方で表すと
図６
となります。Ｅ軸上の実体である単極Ａと単極Ｃは「対」を形成しており、双極Ａ－Ｃです。実体は座標を持たないので単極Ａと単極Ｃは図５右のように同じ位置に書かねばいけないのですが、双極であることを示すために少し離して書きました。 双極Ａ－Ｃが「回転と積分」を伴ってＭ軸に投影されると電子（単極Ｆ）として現れます。 電子（単極Ｆ）はＥ軸に直交しています。そしてＥ軸上の実体である双極Ａ－Ｃのうち、単極ＣはＭ軸上の単極Ｆの位置にあり、一方の単極Ａは「斥力」により遠方のＡ’としてＭ軸上に現れます。その際Ａ’は「直交」している為に図４凡例右に従って小さな●印を入れて表します。 図６は見方を変えると図５の右と同じです。つまり、図６のＭ軸が湾曲しているに等しい訳です。
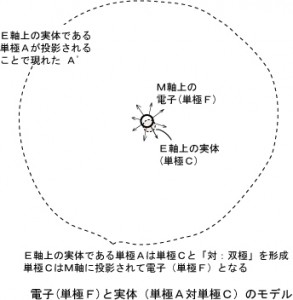
さて、図６の自由電子モデルを我々の３次元空間（Ｍ軸）に置き換えますと
図７
のようになります。 電子（単極Ｆ）は質量や電荷あるいはスカラーポテンシャルを持ち、電気力線が放射状に生じます。単極ＣはＭ軸上では電子（単極Ｆ）と同じ位置になります。 Ｅ軸上の実体である単極ＡはＭ軸に投影されることで電子（単極Ｆ）から見て「無限遠」の位置に座標を持ちＡ’として現れます。電子（単極Ｆ）から見るとＭ軸上に現れたA’は全周囲の位置になります。 何故なら双極Ａ－Ｃには斥力が働いており、かつ
図８
Ｅ軸はＭ軸に直交しているからです。 この辺の理解はかなり難しいです。４次元は難しい。 しかし、数学の無限大（∞）とは若干意味が異なります。
表１
電子の古典的半径は10^(-15)ｍですし、 Ｅ軸上の単極Ａが「斥力」により投影されて位置する無限遠は10^27ｍ程だと考えられます。 電子の大きさから見ると10^42倍程になり、事実上「無限遠」であるといえます。
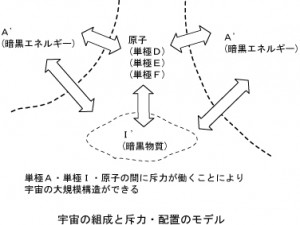
弧理論においては、このＡ’が暗黒物質または暗黒エネルギーだと考えられます。
宇宙の組成は、暗黒エネルギーが６８．３％、暗黒物質が２６．８％で原子等が４．９％だといわれます。
図９
物質を構成する原子｛陽子（単極Ｄ）・中性子（単極Ｅ）・電子（単極Ｆ）｝は暗黒エネルギーと暗黒物質からの斥力により大規模な構造を持つと考えられます。大きな構造は、組成の成分比率により決定されるといってよいでしょう。
「E軸上の実体は座標（空間での位置）を持たない。投影されて初めて座標を持つ」と定義することは非常に興味深いです。 実体が投影されることにより初めて座標が決定されるのですから、物質でできあがった我々が「宇宙の端」や「宇宙の外」に到達したと思っても「そこは宇宙」ですから。 理論的に外に出ることも、考えることも出来ないということです。
西遊記に出てくる
お釈迦様の手のようです。実に面白い。
上記が開放系の力学であることに注意下さい。弧理論は、宇宙の構造を示しているのみであり、「宇宙の外」や「多元宇宙」には言及していません。
あと陽子（単極Ｄ）と中性子（単極Ｅ）がどのように表されるかについては次回に記します。それと、ベクトルポテンシャルとスカラーポテンシャルが宇宙の構造の中でどのように配置されているかを示します。
Follow me!
