本サイトの主旨は弧理論(Ark Theory)の解説ですから、何度も記します。 一応、理解しているのは管理人のみだと思いますので、多くの人にご理解いただけるよう出来るだけ簡単に。 しかし、これが実に難しいです。
一番大事なことは、運動する物体は、静止するに「2つの経路をたどる」ということです。
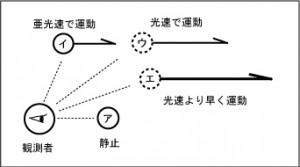
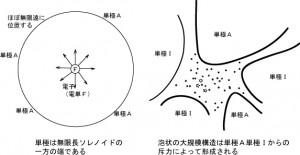
図1
の様に、ある観測者に対して静止している物体(ア)及び、光の速さより遅い物体(イ)と光の速さを持つ物体(ウ)、さらに光の速さよりも早い物体(エ)があったとします。 勿論、運動は相対的ですので、周囲にこれらの物体が存在するからこそ何が何に対して運動しているのかが判別できます。 また、弧理論では相対性理論を否定しています。(時間[T]を含むからです。)
弧理論では、ある観測者に対する運動の状態を4つにわけます。(ア)静止、(イ)亜光速で運動、(ウ)光速で運動、(エ)光速より速い運動の4つです。 そして、光の速さを「音速の壁」のように一つの閾値(しきいち)だと認識します。
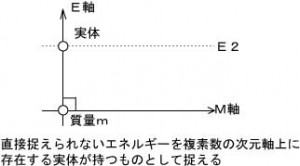
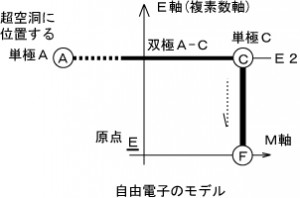
まず、ある観測者に対して物体が静止(ア)している場合
の様に、E軸上の実体が「積分を伴う回転投影」により、M軸上に質量mを持った物体として現れます。これまでご紹介したある科学者が述べたように、「物質はエネルギーに転換するし、逆にもなる」という解釈は誤りで、本当は「一つの実体の異なる側面に過ぎない」からです。実体が持つ真のエネルギー値「E2」に応じた 質量がmとして現れるのです。このときE軸とM軸となす角度は90度です。
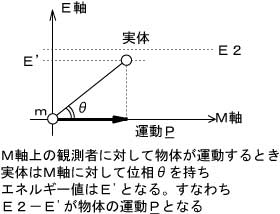
次に、光より遅い速度で運動する場合
の様に、投影の角度θになります。実体が持つ真のエネルギー値は、(E2-E’)減少し、減少分が運動Pになります。ただし、図2において、”弧(Ark)”を描いていません。
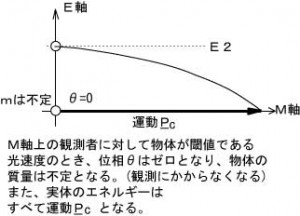
次に、図1の物体(ウ)が光の速さの場合
の様に、投影角θはゼロになります。このとき、物体の質量は観測者からは見えなくなります。(次元軸を失う。例えていえば映画館のスクリーンを舞台袖から見るようなものです。) ただし、E軸上の実体はM軸に平行となることで、質量を持つ物質とは認識されません。M軸上には”弧 Ark”のみが現れます。 図1で観測者から見て、質量を観測できないので物体(ウ)と物体(エ)を破線で描きました。 そして、物体(エ)が光の速さより早い場合も”弧 Ark”が生じます。
ここまでが前提です。
(1)静止した物体(ア)を次第に加速したとき、閾値である光の速さまで加速できません。物体(イ)は図2の状態から図1の状態に戻ります。(減速する)
(2)光の速さの物体(ウ)は、その状態のままです。(電磁波)
(3)光の速さを超える物体(エ)はより速さを増して「”弧 Ark”とともに無限遠に消失する」ことで静止に至ります。
上記、(1)と(2)は理解が容易ですけれど、(3)が問題です。静止の状態では、”弧 Ark”はE軸においてM軸と平行でした。
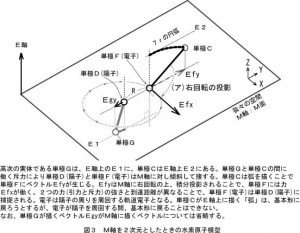
の様に、自由電子(単極F)の実体である単極Cは宇宙の大規模構造を成す単極Aと「双極」を形成するからです。平行な2直線の交点は、無限遠にあります。静止の状態に戻るには交点(弧がM軸上に作る”場”)は、無限遠に消失して静止するのです。 その際に、物体を引っ張るのです。
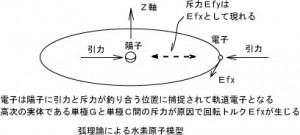
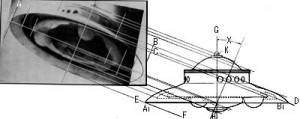
に示した、半径7rの”弧 Ark”が平行に戻ろうとする力Efy「(斥力)=無限遠に引っ張る力」がM軸に「積分を伴う回転投影」によって、回転する力Efxとなって現れるのです。
のEfxが、それです。
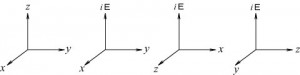
E-M軸の4次元は4つの3次元空間
に分解できます。ここで、図6の軌道電子が回転面を図7左のX-Y平面にあるとします。するとZ軸にE軸が平行に存在することが左から2つめの図から理解できます。(Z軸にE軸が重なる) 図5のE軸上の実体(単極C)と図6の電子とを見比べてください。 図6の軌道電子は、原子核にある陽子の軌道上のいずれの位置にあっても、E軸上からM軸に伸びる”弧 Ark”が静止(90度)の状態に戻ろうとする為に、「斥力:回転する力」を及ぼすことを理解ください。
左図の様に、電子にとって「対」となる単極Aは3次元空間でいずれの方向に存在するかを特定することはできません。昨日の記事参照ください。 原子核近傍にある電子に働く斥力は原子核の方向に直角に回転する力として現れます。
かつて、G・アダムスキーは、「静止しようとするが故に運動する」と講演会の質疑で述べたと記録にあったように記憶しています。 彼の真意はここにあります。弧理論による宇宙の主たるエネルギー源は「斥力:回転する力」に他なりません。
繰り返しますと、閾値である光より速い物体は質量を特定できず、静止しようとするが故に”弧 Ark”の力に引っ張られ運動を続けるのです。 平行な90度(静止)に戻ろうとするから回転するのです。
宇宙の根源的エネルギー源は”弧 Ark”にあります。
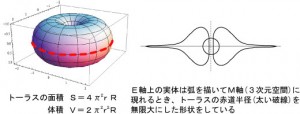
「弧 Ark」の3次元形状は、これまでの考察から
右図の様な、トーラスの外周半径を無限大にしたようなものだと推測しています。外周部分が引っ張られる方向です。この形状はトーラスのように閉じていません。詳しくは第3起電力のエネルギー源について管理人が考察したレポートをお読みください。
どなたか、図8右図をきれいなCGで描いていただけるとありがたいです。 勿論、レンズ状の図形は
にそのまま適用できます。
ブログランキングの応援と広告のクリックをお願いします。