前回の記事の最後に、Ｅ－Ｍ軸平面での「投影」を万華鏡の「反射」に例えました。 この弧理論の考え方を電磁気現象に適用したのが、超効率インバーター「デゴイチ」の「第３起電力仮説」を扱った「第３起電力のエネルギー源について（第２版）」（考察）です。 要点は以下です。
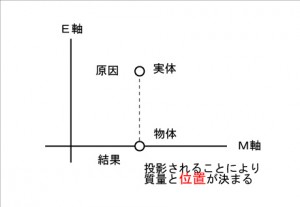図１
我々の存在する３次元物理空間（Ｍ軸）に直交するＥ軸上の実体は、「積分を伴って回転投影」されます。 これにより、物体が質量と位置を得ます。質量は実体が持つ真のエネルギー値に等しいです。
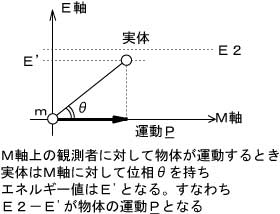図２
ある観測者に対して、物体が運動Ｐしているとき、実体が持つ真のエネルギー値は（Ｅ２－Ｅ’）だけ変化します。減少分が運動Ｐとなります。 物体を加速しようとすると実体は、Ｅ－Ｍ軸平面上を時計方向に傾き投影角θは浅くなります。 θが浅くなるほど加速しにくくなり、投影角をゼロまで加速することは不可能です。
電磁気現象は、電磁交換を特徴としています。必ず直交して現れます。電磁気現象をＥ軸上の実体の変化（Ｅ－Ｍ軸平面での位相の回転）として表したのが表題の考察でした。
回路に電流を流すということによって、Ｅ軸上の実体とＭ軸上の物体（この場合は電子）は
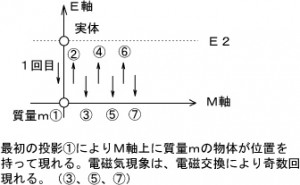図３
のように投影を繰り返します。 質量を持って現れる投影を①としますと、コイルに電流を流すことにより、Ｅ軸上の実体は影響②を受けて、再びＭ軸上に③として投影されます。以後、電流の変化は奇数回⑤あるいは⑦として現れます。 このときのＥ－Ｍ軸平面での位相の変化は
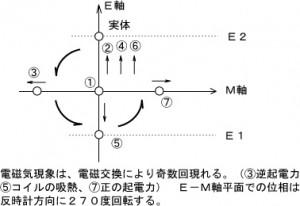図４
の様になります。 Ｅ－Ｍ軸平面での位相は、反時計方向に③、⑤、⑦の様になります。③がＭ軸上において、逆起電力として現れます。そして、⑤がＥＭＡモーターで現れたという「コイルの吸熱現象」の原因のようです。そして、⑦がコイルに与えた「急峻なパルス」により現れるもので、これが「正の起電力」にあたります。 このときのＭ軸上における⑦の形状が
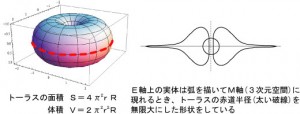図５
右に示した発散トーラスです。 図３と図４のＭ軸上に現れた⑦の実体は、質量を観測できません。何故なら図１において、実体はＭ軸に直交していたものがＭ軸上では平行だからです。Ｍ軸に⑦の状態にある実体が持つ真のエネルギー値はゼロです。全て運動Ｐになっています。その意味でＥ＝ｍｃ＾２（の解釈）は正しいのでしょう。
Ｍ軸上に現れた実体は、これまた質量を観測できない状態にある電子を正の方向に引っ張りながら無限遠に消失します。これが正の起電力⑦の正体ですし、形状が発散トーラス（図５の右）だということです。 無限遠に消失した実体は、Ｅ軸上に戻るとともに、電子も静止状態①に戻ります。 図２と図４を見比べると分かりますが、加速しようと（Ｅ－Ｍ軸平面で時計方向に位相を変化させ）ても投影角θをゼロにすることはできません。パルスを与えることにより、Ｅ－Ｍ軸平面での位相を反時計方向に回転させることができます。そして、⑦の状態から①の状態へは、反時計方向に戻るということになります。都合、位相は１回転することになります。 ただし、ある科学者が述べた「エネルギー軸を中心に全質量を回転させる」ということの意味は、上記とまったく異なります。
無限遠に消失した実体（複数種）の持つ構造が
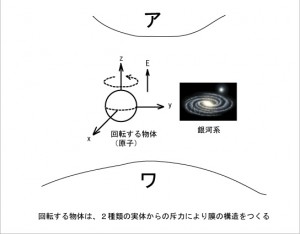図６
や
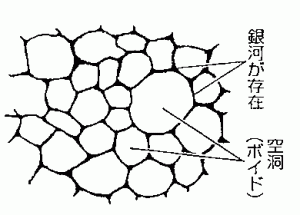図７
の様なものです。
Ｅ軸上の実体は、Ｍ軸上では位置を特定できません。「位置を特定でない実体は、物体への斥力がもとで大規模な構造を作る、と同時に原子の構造を左右する力として至近距離に現れる」これが「距離の７乗に逆比例する力」だと考えられます。 直感的には、カシミール効果と何か関係ありそうに思うのですけれど。
前回の繰り返しになりますが、自然が対称性を持つことと離散値をとること、それとデゴイチに正の起電力があり得ることも全て繋がっています。 まだよく分からない部分も・えいやっ・で記述してます事をご了解ください。
Follow me!
