我々は時間という観念に縛られています。これまでの考察により時間は存在しないことが分かっています。 あえて定義すれば
-
時間とは、過ぎ行く運動の記憶である。
私たちが肉体に備わった五感で分かるのは運動だけです。 にもかかわらず自然科学者たちは、時間は存在すると信じて疑いません。 既に２００年ほども経ってしまいました。自然科学はこれから何処へ向かうのでしょうか？
いつも引用するある科学者の言葉を列挙します。以下、青字強調は管理人によります。
我々は君の国の多くの一流科学者の精神を調べてみたんだ。大抵の場合、我々は科学者たちの精神が既成概念という鋳型で固められていることを知った。彼らは遠くまで進みすぎている。その結果、遠い道のりを後戻りしなければならない。 －略－ 科学知識を求める人間は木に登るアリのようなものだ。自分では上方へ動いていることがわかっていても、その視野は狭すぎて幹全体を見通せない。そのために幹を離れていることに気付かないで下方の枝の方へ移動するかも知れない。一時は万事うまくゆく。自分ではまだ上方へ登れるし、進歩という果実を少し摘み取ることもできる。だがその枝が急に無数の小枝に分かれていろいろな方向に葉が散らばっているために本人はまごつき始める。 －略－ 基本的法則がいまや分かれはじめて、反対方向に散らばり始めていることに気付く。すると科学者は心によって受け入れられる知識の限界に近づいていることや、あらゆる物理的な法則は究極的には全く統計的なものになるという結論に達する。これは地下鉄の列車に乗っていくようなものだ。たぶん最後には目的地に着くだろうが、どこへ行くのかが分からないために、同じ場所へ着くのにもっと短くて容易な方法があることを確かめられない。
「基本的な法則が反対方向に散らばる」というのは、
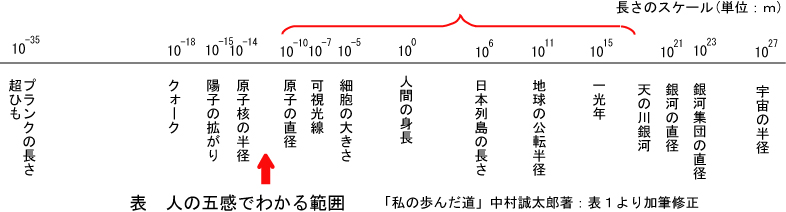
表１
相対性理論と量子力学のことを意味していると考えられます。上表の左右はうまく統合できていません。 「心によって受け入れられる知識の限界」とは、数学を用いて抽象的な表現により研究を進めている状態をいうようです。 また、「物理的な法則は究極的には全く統計的なもの」というのも、そのとおりです。
正しくながめれば基本的な真理はかんたんで理解が容易なのだ。だから幹の上からながめれば枝は”枝”としてかんたんな理解の容易なものになるのだ。てっとり早く言えば、君らの科学が進歩し続けようとするために必要なのは、君たちがとまっている枝から幹との分岐点まで降りて、ふたたび登り始めることだ。
ある科学者は、基本的な法則は簡単であり理解は容易だと述べています。運動あるいは距離を時間に置き換えるということを、既に２００年以上続けてきました。本当に遠くへ行きすぎていると感じます。これからどうするのでしょう？ 「たぶん最後は目的地に着くだろうが」と否定的に述べています。 そして、次のように述べています。
物質科学の進歩を止めることなどできやしない。それは進んだりもどったりはするにしても。もどるとすると、それを支えている要素は退化のプログラムによってまず弱くなってきてそして崩壊することになる。 基礎的には地球の物質科学に悪いところはないんだ。もし、人々がそれを支えることができるような基礎を用意しないとそれは夢想だにしなかったほど水平に広がって進歩してしまう。「もし、基礎がなかったら？」 －略－ 「君たちの文明は終わるさ」
退化のプログラムという考え方は、１９５０年代には存在しなかったと思われます。アポトーシスは、wikiによれば２０００年代に入ってからのことです。
理解が容易な物理法則を我々が基礎として用意できなければ、文明は終わると警告しています。 「夢想だにしないほど水平に広がって進歩」とは言い得て妙です。
こちらから拝借
ビッグバン理論や
こちらから拝借
超弦理論など、水平に広がっていることは理解できます。 このまま行きますと、退化のプログラムによって弱くなり、やがて崩壊するようです。 そのとき基礎となる物質科学を用意できれば、再び進歩が可能だということです。
これまで、３次元物理空間での様々な現象を、
こちらから拝借
万華鏡に例えてきました。３枚の鏡を組み合わせたものです。
こちらから拝借
内１枚を幅の小さなものに変えますと、模様の繰り返し数が多くなります。
.
動画１
のように、模様の繰り返し数とともに、画面の「端」にも模様の繰り返しが続きます。 一方で、二等辺三角形の一辺、幅の短い部分を黒い紙に置き換えますと、画面の「端」には模様の繰り返しはなくなり
．
動画２
の様になります。周辺が黒くなります。
宇宙における現象を万華鏡に例えるならば、動画１の様なものがより近いです。対称性の内に「端」を見れば模様は続きますが、次第にはっきりしない模様になっていきます。模様は続くだろうけれど、はっきりしません。自然科学者は何を目指しているのでしょうか。
ちなみに、管理人所有の万華鏡は、
の様なものです。二等辺三角形の３枚とも鏡ですので、動画１のように「端」にも模様の繰り返しが続くものです。とても綺麗です。
Follow me!
