量子もつれについては、過去に何度か書きました。量子もつれについて画像検索しますと様々な説明がなされていることがわかります。 改めて量子もつれの弧理論での考え方を記します。
弧理論の考え方は、３次元物理空間とは余分の次元軸が存在するとしています。４番目の次元軸をＥ軸としています。分解すると
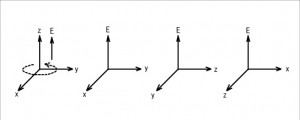図１
のように、４つの３次元空間に分けられます。物質の質量とその運動は、別の次元軸上に存在する一つの実体の異なる側面です。この運動は、物理学で定義されるエネルギーです。次元解析では[ML^2T^(-2)]と表される量です。ここで時間軸も時間[T]も存在しませんから運動をエネルギーといわずにＰと表します。 ３次元を横軸にＥ軸を縦軸とする２次元平面で描くと
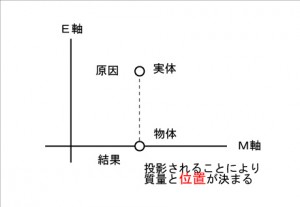図２
のようになります。Ｅ軸上の実体は位置を持ちません。実体と物質との隔たりを時間を含まない真のエネルギーと呼びます。だから余分な次元軸をＥ軸と名付けました。
このとき我々の視点はＭ軸上にあります。ここで視点を実体に移しますとＭ軸上の物体あるいは物質は、
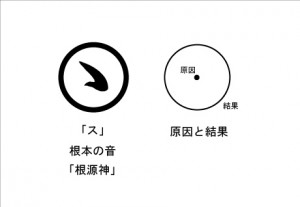図３
右図のようになります。つまり、実体から見ると宇宙のすべての物体あるいは物質は、円あるいは円弧の線上に位置するように見えるというわけです。
いま、一つの実体がＭ軸上に投影されることによって
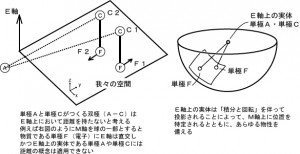図４右
のように２つの単極Ｆ（物質）が生じたとします。これが弧理論に於ける量子もつれのモデルです。２つの単極は宇宙（Ｍ軸）のどのような位置にあろうとも実体は一つであるという説明です。 問題は実体に対するＭ軸の湾曲が球ではなくて「弧」であるということです。
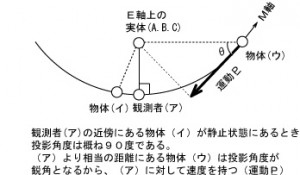図５
のように、２つの単極（または物質）である（ア）と（イ）が比較的近傍であれば、実体から見て投影の角度が概ね９０度同士です。離れることによりこの角度が９０度以外になり「もつれ」が解消されると考えられます。量子もつれの突然死と呼ばれる現象です。
次が分かり易い説明になります。 いつも弧理論の考え方を説明するとき
.
動画１
万華鏡に例えています。動画１のある瞬間をキャプチャしたのが
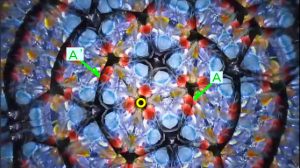
写真１
です。画像は中央付近の黄色い丸印を中心と考えたとき「対称」を示しています。 右にある赤い点々「Ａ」に注目します。 似た画像が左に「Ａ’」として見えます。 画像は刻々と変化しますし、ＡもＡ’も似た変化をします。ここでＡとＡ’の距離を考える人は居ないはずです。何故なら、万華鏡に見える画像の変化は対称性があるとともに、距離が関係しないことの理由がその構造にあることをを誰もが知っているからです。見える様とその原理が異なるということを皆が知っています。
量子もつれは例えていえば、写真１のＡとＡ’の関係に似ています。図４右、図５の様に考えれば「空間での距離」は関係がないことが理解できます。 量子もつれは、量子論において高度な数学的記述によってはじめて理解することができるとされます。不思議な現象ですけれど、本当は至極簡単であろうとというのが弧理論の考え方です。
ついでに記せば、動画１は対称性を示していますけれど、画像の端へ行けば行くほど、対称性はぼやけ不明瞭になり、遂には判別できなくなります。これは前回記事で記した「五感の地平線」に似ています。 図５において、観測者（ア）の持つ五感で「分かる」のは、近傍にある（イ）であり、極めて遠くの物体（ウ）は、運動Ｐを持っていることが分かります。（観測者に対して９０度以外の投影角を持つ場合、観測者に対して運動していることを示す。） この（ウ）は宇宙の地平線（事象の地平線）を示しています。また、極微の原子や素粒子も示しています。何故なら極微の世界も観測者に対して浅い投影角を持って運動Ｐをしているからです。 図５の（ウ）は
表
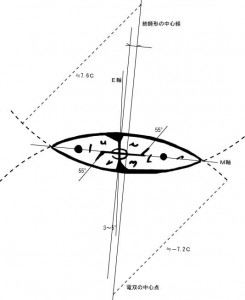
の両端を示しています。弧理論の考え方は、表のこともよく説明できます。 図２、図３右、図４、図５の元となった図を下に示します。
Follow me!
