何も 実験 が危険だという意味ではありません。落語「饅頭こわい」を模したものです。
動画１
２０１６年１０月末に弧理論の核心部分がわかって、２０１７年にかけて全体像（精神科学・社会科学・物質科学）が見えてきました。 ３つの科学は同時に進めねばなりませんので、今年に入ってからは、主に物質科学について考察を進めてきました。
主にファラデーの単極誘導モーターについての実験でして、これまで思惑どおりにいったことがありません。それでも数式に表されていない現象を観察したのですから、一定の成果があったと考えています。
今回、あるアイディアに行き着いて「井出治氏による超効率トランス（第３起電力のエネルギー源について）」に関する考察から得られた発散トーラスの（複数の）
組み合わせによって、いわゆるローレンツ力と同じ現象を示すらしいことがわかりました。（井出治氏のトランスはローレンツ力に関係する可能性があるということです。） ようやくアイディアを実験レベルに落とせたのですが、やはり実験で「思惑どおりにならずに失敗する」かどうか確かめるのが怖いです、という意味の実験こわいです。
それにしても実験は億劫です。
参考図と解説
いわゆるＥ＝ｍｃ２について、ある科学者は次のように述べています。「物質はエネルギーに転換するし逆にもなるというが、本当は一つの実体の異なる面に過ぎない。」 （注：物質は別の実体が投影されることによって現れる映像だということです。）
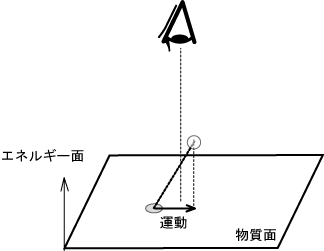図１ 物質の質量と運動は実体の投影による映像
これが別の次元軸を考える根拠です。別の次元軸をエネルギー軸とします。以下、Ｅ軸という。 そして、別の次元軸上にある実体の持つ値を真のエネルギー値とします。 一方で、物理学で定義されたエネルギーを運動Ｐとして、真のエネルギーと区別します。 別の次元軸（Ｅ軸）は、空間に直交します。ですので、一般に運動する物体にかかるＥ軸の方向を特定することはできません。
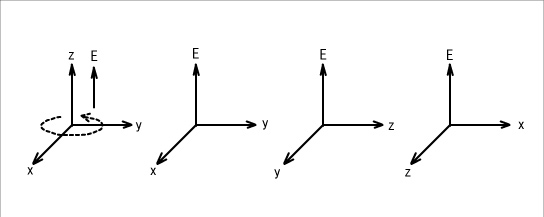図２
唯一の例外があります。 図２のように４次元は４つの三次元に分解できます。 空間で運動する物体に直交する方向にＥ軸は存在すると考えますので、ｘｙ平面内で回転運動する物体にかかるＥ軸は、ｚ軸方向に重なります。
発散トーラスには４種類あります。
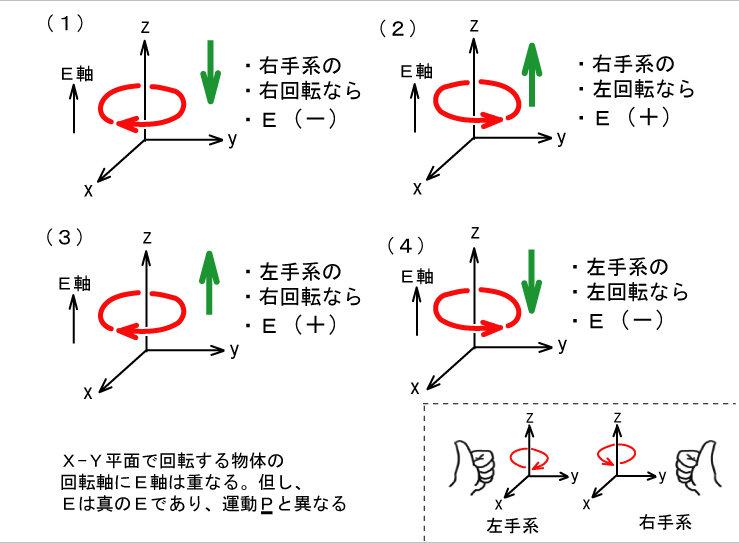図３
４種の内、２つがＥ（＋）で２つがＥ（－）を示します。 回転体においては、これがｚ軸に重なるということです。
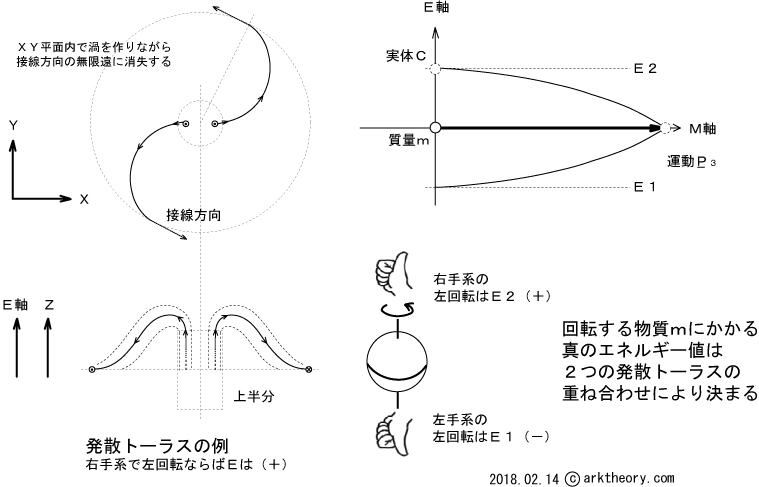図４ 右上に示した弧（Ark）のＭ軸との接する部分の空間での形状が発散トーラスである。
回転する物体の真のエネルギー値（Ｅ２－Ｅ１：差分）は、２つ発散トーラスの組み合わせによります。 図において、左回転の物体の例を考えると「右手系、左回転」では、真のＥはプラスです。これがＥ２です。「左手系、左回転」での真のＥはマイナスです。これがＥ１です。
弧理論によれば物体は、このＥ２－Ｅ１の値に相当する重力を持つことになります。これはあたかも表面張力による引力斥力に例えられます。だから他の３つの力（電磁気力、弱い核力、強い核力）とは格段に弱いのです。 重力は質量が原因ではないとの結論です。
動画１
また、物質の真のエネルギー値は、二層型の浮沈子に似ています。
動画２
浮沈子の浮き沈みの具合（真のＥ＝Ｅ２－Ｅ１）が、物質にかかる図２の発散トーラスの組み合わせによる回転の具合いにかかっているということです。
ＥＭＡモーターの回転軸から出ているケーブルの意味がようやくわかってきました。モーターは回転軸方向に非対称である必要がありそうです。 放電に関しても疑問がありますが。
写真１ 出典:Electro-Magnetic Association (EMA) Motor より
面白い記事がありましたので、メモします。 「フリーエネルギー監視委員会＿ほとんどがニセモノです！」のサイトより、2018年4月28日 井出治氏の超効率インバータの続報 とのことです。第３者による追試がうまくいっているようです。
パルスかあるいは磁気回路を非対称にするなどのノウハウがあると考えます。（２つの発散トーラスが打ち消し合うため。如何にバランスを崩すかがカギです。） 勿論、測定器の誤差かも知れません。 リンク先のReplication of the Ide transformer deviceやDetailed measurements of Ide transformer devicesではよくわかりません。
大事なのは、真のエネルギー値と、物理学上のエネルギー[ML2T-2]を区別して考えることです。 エネルギー保存の法則は、質量と運動Ｐの関係を述べたに過ぎません。（図１を参照ください。） （真の）エネルギーの量を正しく計る方法を知らないのです。
どうでもよいこと。
ローレンツて何者でしょうか？ マクスウェル方程式を（非対称な部分を切り捨てて）現在の対称的なベクトル表記にした人物がローレンツ。 電磁気学におけるローレンツ力のローレンツ。 そして、相対論の元になったローレンツ変換のローレンツ。
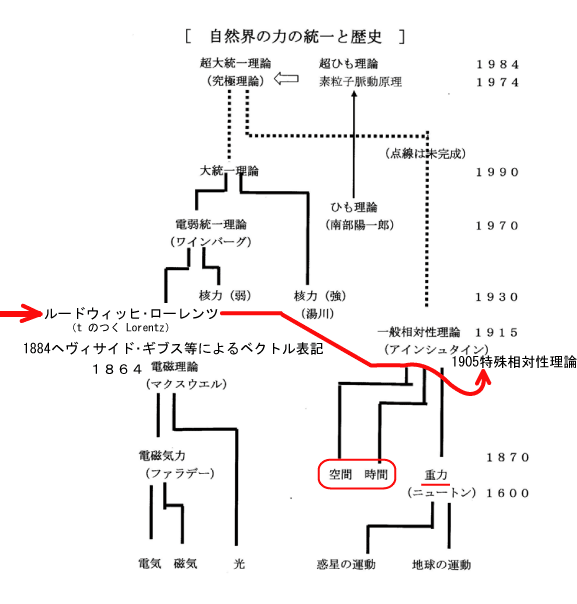図５
複数人いることはわかっていますが、歴史上大事な時期に出てくるのが「ローレンツ」。一体何者だろうか？ ファラデーが発見した単極誘導の現象を無かった事にしようとしたように見えるのは管理人だけでしょうか。 その意味でトム・ベアデンはディスインフォーマーではないかと疑ってしまいます。スカラー波からは何も出てきません。
．
Follow me!
