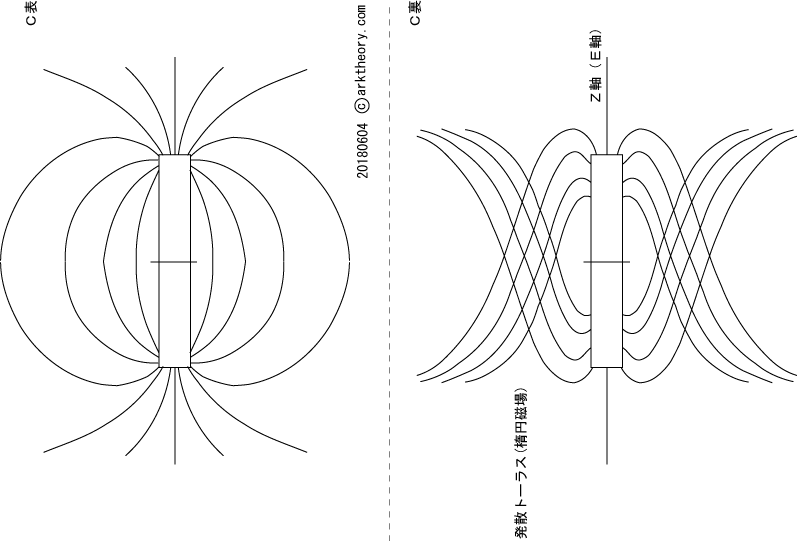
Ｇ・アダムスキーが述べた技術的な用語に 楕円磁場 や静電気などがあります。この語は技術ふうではあっても、電磁気学に合致したものではありませんでしたので、誰も本気で考えたことはなかったようです。 今年に入ってから弧理論による物質科学に関して考察を続けてきました。 今回、発散トーラスを組み合わせることによってできる 楕円磁場 のモデルを考案しましたので記します。
２０１３年頃、井出治氏によるパルストランスにかかる超効率の第３起電力仮説を考察した「第３起電力のエネルギー源（考察）」によって見いだしたのが、発散トーラスでした。形状は磁場に見られるトーラスの半分に渦を巻いた格好をしています。
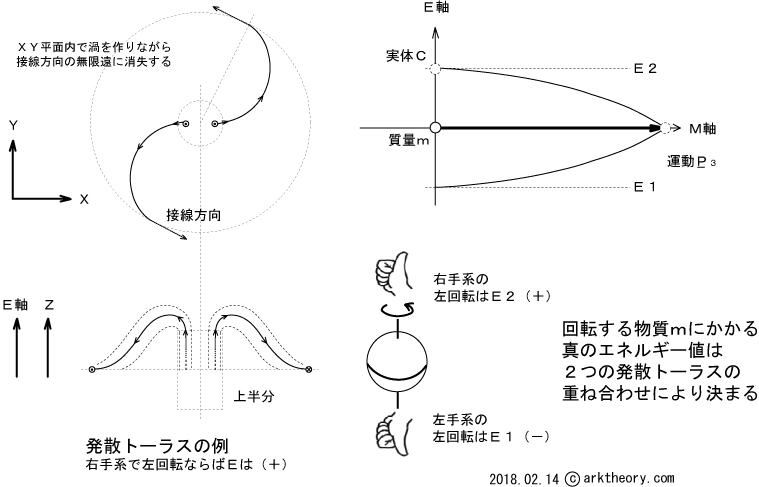図１
発散トーラスは４種類に分けられます。
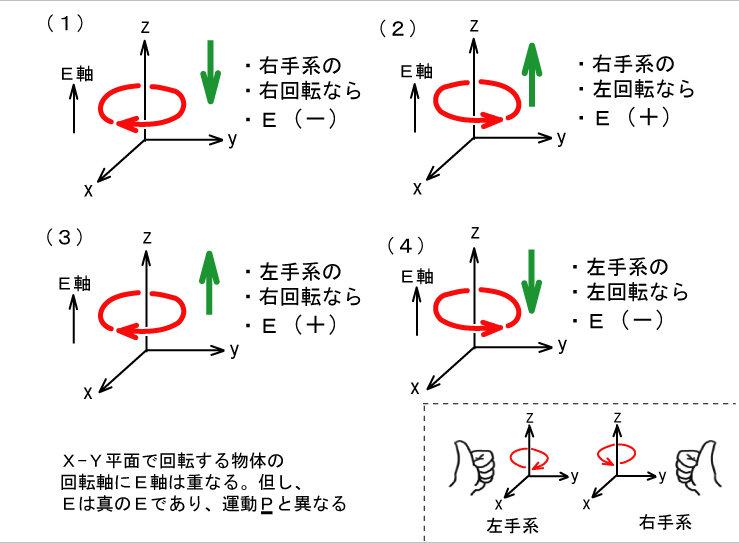図２
回転する物体の回転軸（ｚ軸）にＥ軸上が重なります。何故なら、ｘｙ平面での回転ならば、Ｅ軸は運動面に直交するからです。
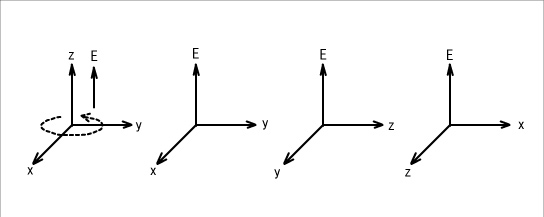図３
３ＤＣＧにしたのが次です。
わかりにくい説明で申し訳ないのですけれど、全ての物質や波は別の次元軸からの投影による映像だというのが弧理論の核心です。別の次元軸をＥ軸と呼んでいます。基本形は次のようです。
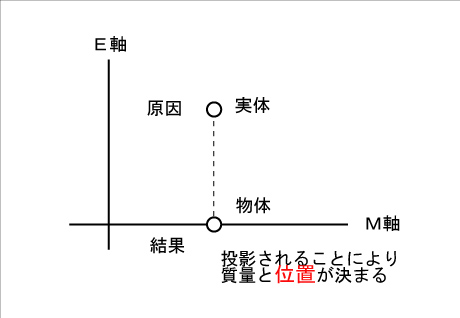
Ｅ軸上の実体が原因。物体は結果。
図４
Ｍ軸が我々の居る物理空間です。 Ｍ軸を二次元平面で説明したのが次図です。
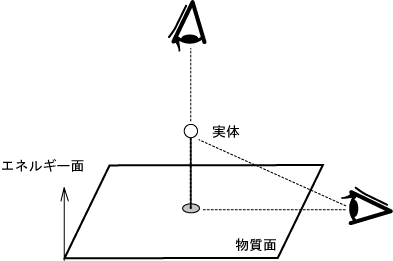図５
我々は視点を移動するのではなくて、Ｅ軸上の実体のＭ軸上への投影角が変化したと考えます。
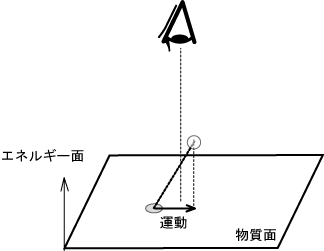図６
上図の運動Ｐというのが物理学で定義されたエネルギーに相当します。 実体が持つ値を真のエネルギーと呼び、物理学上のエネルギー（運動Ｐ）と区別します。注：運動Ｐは時間を含みません。
有名なＥ＝ｍｃ２という式の意味がここでわかります。Ｅ軸上の実体が持つ真のエネルギー値は投影によって物質の質量ｍとして現れます。投影角が鋭角になるに従い運動Ｐとして現れます。 ということは、『質量は運動Ｐ（物理学上のエネルギー）に転換するし逆にもなる』というのではなくて、本当は、「Ｅ軸上の実体が持つ真のエネルギーは、質量と運動Ｐの両方の面を持って現れている」という事になります。 Ｅ＝ｍｃ２という数式の意味の解釈はまったく異なってきます。
上記の説明では不十分なことは承知していますが、続けます。 井出氏のトランスにおいては、コイルにパルスを印加する際に、Ｅ軸上の実体の投影角が鋭角になり、１つの発散トーラスが生じると考えました。 考察を続けた結果、物質は常に２つの発散トーラスの組み合わせによってＭ軸上においては、真のエネルギー値は常に打ち消し合っていることがわかりました。
従前、発散トーラスは次のように表していました。（図７右）
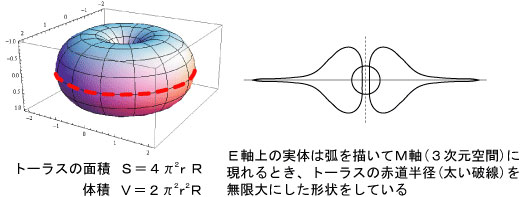図７
発散トーラスは、上半分もしくは下半分しか生じないと考えてきました。 しかし、フリーエネルギー研究家トム・ベアデンによる手紙「Tom Bearden’s Response to ARPA-Eビールデン博士のエネルギー先端研究局への返答」には、互いに打ち消し合っていると述べられています。一部引用します。
10． その後間もなく，ヘビサイドは比較的小さな発散性ポインティング成分に加え，あらゆる電池や発電機の端子から放出される巨大な回転性電磁気エネルギー流を発見しました。このヘビサイド回転成分の大きさは，比較的弱いが発散性であるポインティング・エネルギー流成分よりも 1 兆倍以上も大きいのです！ 任意の座標系（特殊相対論の状況）において，回転の発散はゼロです。そのため，通常このヘビサイド成分 – 発電機のシャフトを回す単位時間当たりの機械的エネルギー入力の 1 兆倍以上 – は，何かと相互作用を起こすことも，また外部回路に発散していくこともありません。代わりに，それはただ空間に向かってうなり続け，浪費されます。
ベアデンによれば、ヘビサイドが発見したというエネルギー流は、弱い発散性のＰエネルギー流成分より「１兆倍も大きい回転性電磁気エネルギー流」だと云います。しかも回転による発散はゼロだと云います。何かと相互作用を起こすことなく、外部に発散もないということです。
そこで考えたのが次です。
写真１ 反時計方向の回転を持つ発散トーラスの模型：真のエネルギーは互いに打ち消し合う
写真１は図７右を手で模したものです。打ち消し合っているとしながら、渦が上下に分かれて２つできています。これではダメです。そこで考えたのが次です。
写真２ 左回転
写真３ 右回転
写真２と３は、いずれも真のエネルギーは打ち消し合っています。（親指がＥ軸の方向を指していて打ち消す。） これで、トム・ベアデンが述べた「ヘビサイドが発見した回転性電磁気エネルギー流」に近い、あるいは同じものだと考えます。これが楕円磁場のモデルです。
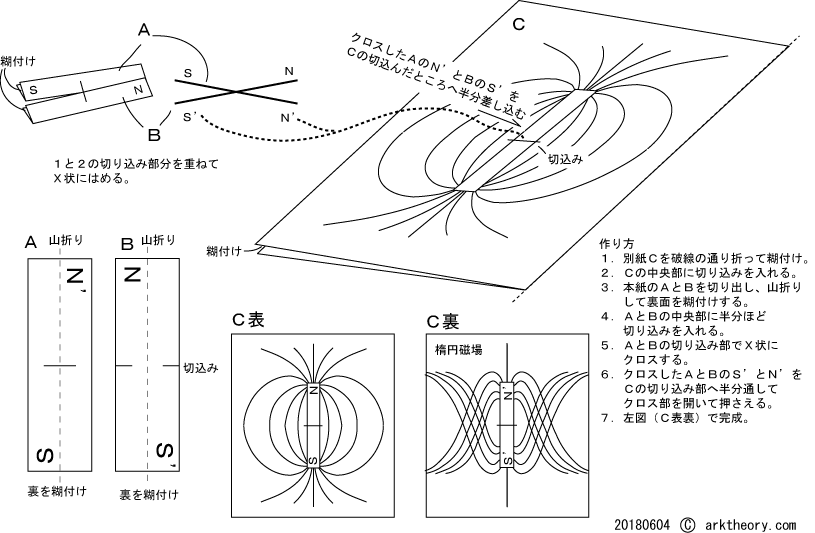
次に、２つの発散トーラスを組み合わせてできる楕円磁場と通常の磁場との関係を示します。 誰がどう見ても磁場（双極）はトーラス状をしていて、Ｎ極とＳ極は対を成しています。 ここで、管理人自身飲み込めないままながら、磁場（表）と楕円磁場（裏）の関係を図に考案しましたが次図です。
図８
図９
図８と９は別窓で開くpdfです。Ａ４横に印刷して使います。要所を切り貼りして作ります。
写真４ Ｃを破線部分で折り、糊付け
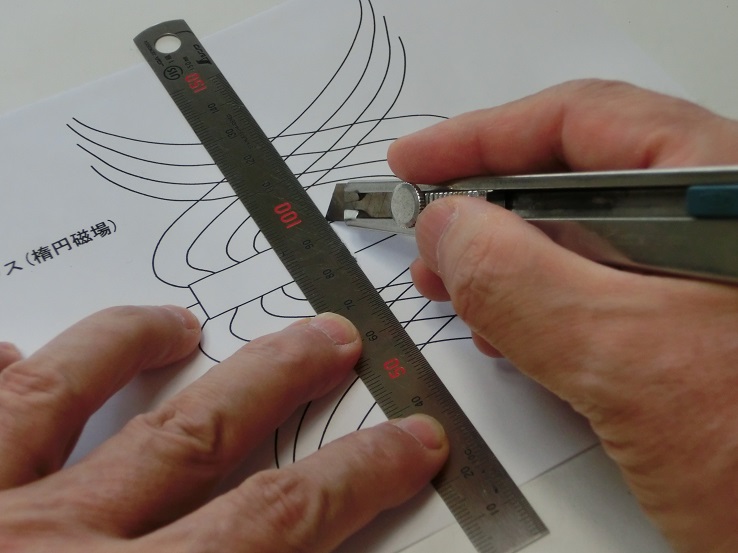写真５ 中央部にカッターで切り込みを入れる
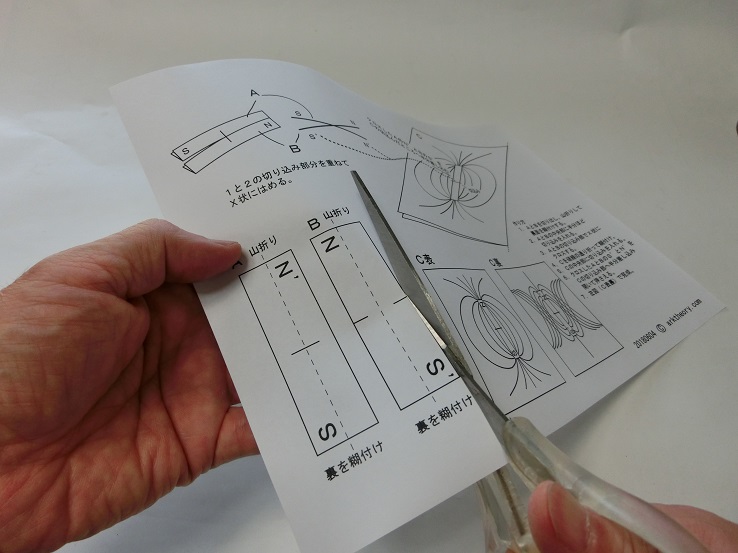写真６ 図９のＡとＢを切り出す
写真７ ＡとＢを山折りにして糊付け
写真８ ＡとＢの中央部に半分まで切り込み
写真９ ＡとＢをＸの形に組み合わせる
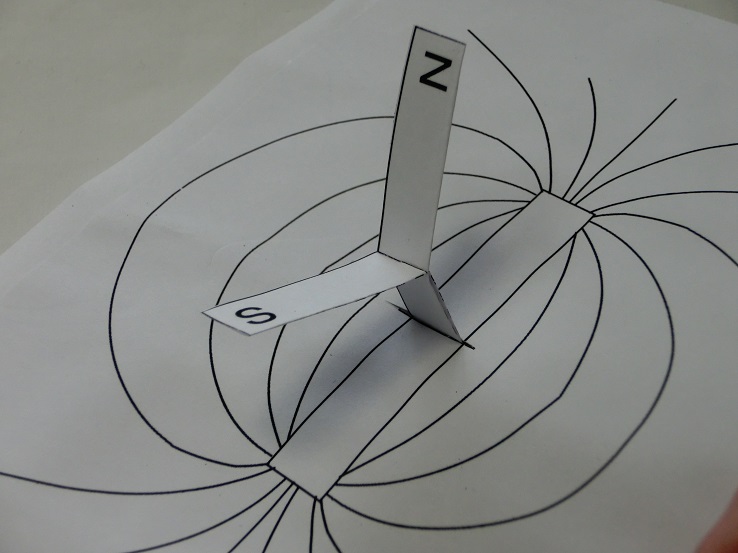写真１０ Ｃの切り込み部にＡとＢのＮ’とＳ’を揃えて差し込む
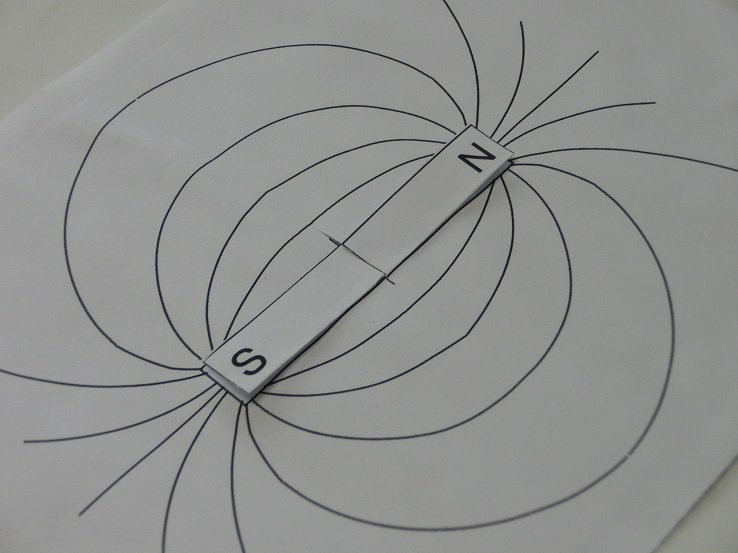写真１１ 組み合わせたＡとＢを広げてできあがり （表）磁場
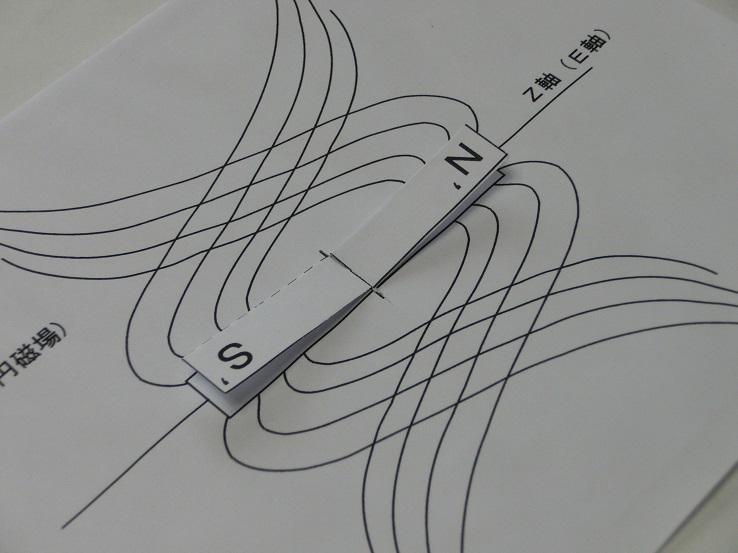写真１２ （裏）２つの発散トーラスを組み合わせてできる楕円磁場 注：Ｎ’Ｓ’は仮の名称
磁石の軸方向（ｚ軸）にＥ軸は重なります。かつ２つの発散トーラスは、互いに打ち消し合っていますので、（裏）の楕円磁場はほとんど観測に引っかかりません。 通常、（表）の磁場しか意識しません。
で、（裏）の楕円磁場なのですが、２つの発散トーラスの組み合わせによって、互いに打ち消し合っているのですが、僅かばかりの差があるようです。これがファラデーの発見した単極誘導の現象なのではないかと推測しています。単極誘導は楕円磁場に原因があるということです。
式１
これで長らく意味のわからなかった点が理解できそうです。 電磁気現象での起電圧がなぜ２つの現象の合算なのかということです。 量子力学ではまったく異なる理由が理論計算で示されている様です。しかし、この様なモデルの方が理解が容易です。このことは重要です。確かにＮとＳが対でなく、発散トーラスの一つと対だと云う考えは、ハードルが高いです。しかし、量子力学における数学の理論計算はごく少数の専門家にしか理解できません。これでは次へ進めるわけがないのです。
これで、次のことがわかります。
電気 ←→ 磁気 ←→ 発散トーラス（楕円磁場） ←→ Ｅ軸上の実体が持つ（真のエネルギー値）
の関係が成り立ちます。つまり、電磁気現象を用いることによって、磁石あるいは物質が持つ真のエネルギー値を制御できる可能性が出てきたということです。私達がエネルギーと呼んで理解していたのは運動Ｐに過ぎません。
物質あるいは物体が持つ真のエネルギー値を制御できるとは、どういうことでしょうか。つまり、磁石のｚ軸方向にＥ軸が重なりますので、ｚ軸方向に真のエネルギーによる勾配が作り出せるということです。
写真１３
通常は、（裏）で楕円磁場は打ち消しあっています。微弱な単極誘導の現象しか観測できません。これをうまく制御できれば、磁石の極の方向に真のエネルギー勾配を作れるはずということです。
ある科学者は述べています。「自然界では多くのタイプのエネルギー発生源がいつも利用できる」とした上で、次のように言いました。
だから望ましい結果を生み出すためにエネルギーの流出を見るような方法を講じさえすればよい。(While this was not always a reliable source, it was sufficiently successful that it should have made your people realize that there are many types of energy differential constantly available and it is only necessary to design a means whereby the flow of energy can be made to produce the desired result.)
やっと見えてきましたけれども、先は長いです。
４本の指が渦を示していますが、４対４で打ち消していますところを、４対３にできればよいのです。説明は簡単ですが、この方法がわからない。
楕円磁場を用いれば、重力の意味も理解できます。相対論とは異なります。空間が曲がるというのに光速度不変を持ち出すのは、まったく奇妙です。
Follow me!
