先日の記事、『岡潔 的思考 右の内耳について』の続きです。どうもわかってもらえません。 岡潔の思考方法は、岡自身の解説から読み取るのは困難です。ほとんどの人が仏教思想とか禅との比較などからわかったつもりになっているようです。 大事なのは実践です。岡潔が指摘しているように、ほぼ誰もやりません。
右の内耳に関心を集めるという、それだけで別の見え方をします。そうすると成程とわかって来るからやってみなさいと云ったんだけど、勿論やらなかったでしょう。やらなかったと云う顔をしてるから(笑いながら)。やったら顔つきが変わる。しかしね、僕の云うことを少し ― 僕は哲学してるんですよ、こういう時はね。それを少しついて来るようになった。だからそういう修業をしたんじゃないでしょうが、だいぶん右の内耳に関心が集められるようになって来たのかもしれない。本当の哲学はそうしなきゃ出来ないんですね。
どうも岡潔講演録の解説に適切なものがありました。「【27】 西洋人の創造」からです。
岡はこういっている。「精神集中をつづけていると、いつしか努力感を感じない精神統一になっている」と。
「努力感を感じない精神統一」、これが管理人の云う「弛緩」です。だからといってサボっているわけではありません。今、問題だと感じていることについて、あれこれ思考しながら関心を持ち続けるのです。 ですから、知恵は頭を絞ることによって出てくるものではありません。知恵は心に浮かぶものです。『聞こゆるを聞き、見ゆるを聞く』とは、そういうものです。決して緊張と集中からは出てきません。
近頃、陸上短距離走において、リラックスした状態で走る方がよい記録が出ることが知られるようになりました。 岡潔は難しいことを述べている様で、実は簡単なことを云っています。 ガチガチに力一杯走るより、リラックスした方がよいのです。貴方は全身に力を込めて考えて(走って)いますか?それともリラックスして考えていますか? 岡潔の話は、スピリチュアル系でもオカルトでもなくメンタルの話をしているに過ぎないのです。 考える際の姿勢のことを云っているのです。
余談です。
「(答えが)わかる」において、「理解する(物の理ことわり)」との違いはここにあります。2018年12月4日『人が持つ「 わかる 」には3つ在る』の結論を再掲します。
人の「わかる」には3つあります。
- 第1の心・・・意識を通す。言葉で云える。わけることによりわかる。要素還元主義。物の理。
- 第2の心・・・意識を通さない。言葉で云えない。何となく趣おもむきがわかる。情じょう。静止画がわかる。ナサケエダ
- 第3の心?・・・意識を通さない。言葉で云えない。何となく動きがわかる。動画がわかる。「もののあはれ」「アワレエダ」
ここで、1.の「わけることによりわかる」には緊張と集中が必要です。しかしながら、新しい「知」である発見は、1.では出てこないのです。
これには、理由があります。物質的自然は互いに規定し合ってできている循環だからです。 おまけに自然科学は時間を用いることによって更に複雑になっています。時間という物理量はありません。
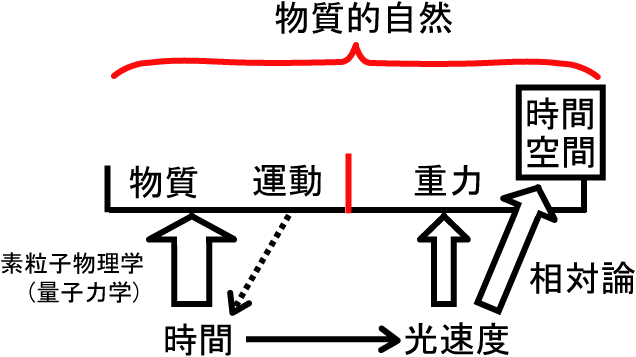 図1
図1
究極、物質的自然は、わけることによってわかることはありません。 専ら「わかる」というのは、直にわかるのであって、「わけることによりわかる」のではありません。これが岡潔の云った2.情じょうです。
言語は互いに規定し合う循環です。ですから、人の思考にも循環の要素が入っています。記号を用いる数学で心を病むのは際限のない循環によると思われます。2018年3月27日の「宇宙の真理を探究するに最適の道具は 数学 だという。ならば何故、数学の難問に挑むと心を病むのだろうか?」を参照ください。
目一杯力を込めて考えてもダメです。「わかる」の本質は2.と3.にあります。
ブログランキングの応援と広告のクリックをお願いします。





大量にある騒々しいパケットを止めれば、本来身体に流れている通信を垣間見れる。応用すると、複雑な問題の解決策が勝手にやってきたり、指先の数十マイクロm^3の空間を拡大して見たり、いろいろできる。
わけだけど、リラックスする方法というのは子供の頃からちゃんと教わっているものではないですね。緊張と集中は身体へのプログラム入力だと思う。
>勝手にやってきた
そうです。関心を持ち続けると、あるとき「ふっ」とやってきます。渦とサイホン、二層型の浮沈子、二層型の逆転渦、これらはみなそうやってできたものです。ただし、発散トーラスは純粋な幾何思考の結果です。
>教わっているものではない
そうです。緊張と集中が解決の唯一の手段だと思い込んでいるだけです。自身、研究を始める頃、やりたいことに対して数学がまったくダメなのに研究の体を成しえるのかわかりませんでした。でも次第に(弛緩と関心による)考察でうまくいくことを学びました。今は逆に数学が目的と手段によっては凄く効率の悪いものだとわかってきました。数学(による証明)は後付けに過ぎません。