２０１０年から宇宙の外とは何かを考え続けて、２０１７年頃にやっと「 外のない内 」という表現に辿り着きました。2017年11月24日『自然科学のいう「非科学的」とはどういうことか？』を参照ください。
発端は、Ｇ・アダムスキーの足跡でした。
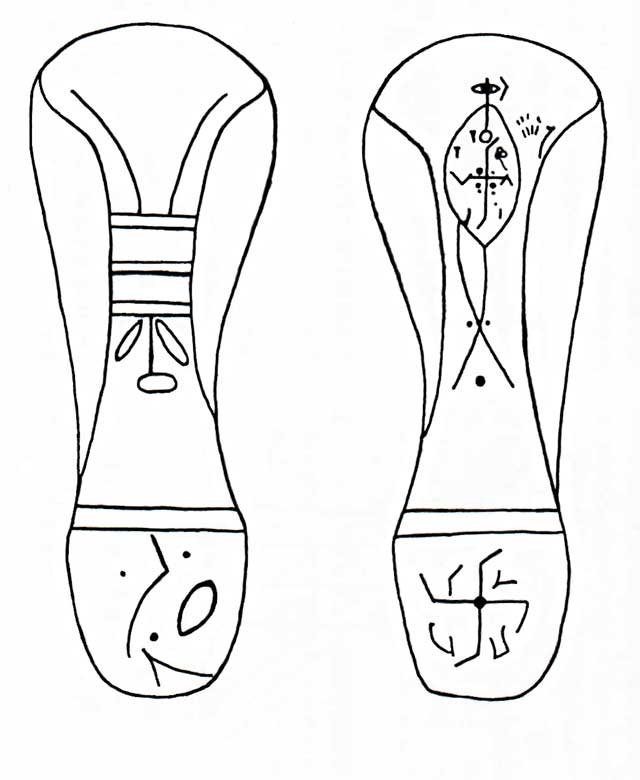図１
宇宙の中に居る我々の存在は、図に示される幾つかの紡錘図形で表されていることはわかっていました。問題は足跡の輪郭です。我々は２種類の何かに包まれていて、輪郭は「宇宙の外について、一切言及していない」と考えていました。当時はそう表現したものの、何かすっきりした言い方は無いかと探し続けてきました。それが２０１７年に山崎弁栄上人記念館の資料の中にぴったりの表現を見つけました。それが「 外のない内 」でした。
ぴったりの言葉がみつかるまで、孫悟空とお釈迦様の掌を例え話に幾つか記事を書きました。サイト内を「孫悟空」で検索すると５件見つかります。説明するに結構苦労して記事を書いています。
一般的に自然科学は孤立系の学問です。（たぶん）一定区間の量を計測し、平均を求めます。後は、数学的にマイナスの無限遠からプラスの無限遠までの積分をとれば全量を求められると考えられていると思います。で、孤立系を無限大まで拡張すれば開放系に等しく扱えると考えているように思います。この考えは管理人の考える自然科学に過ぎないかも知れませんが、自然科学をそのように捉えている方も多いと思います。
一方で、数学を含む言葉（言語）は互いに規定し合うことにより成り立つ循環であることがわかっています。例えば２進数で云えば、”１”とはゼロでない数ですし、ゼロとは”１”でない数としか云えません。
同様に無限大（∞）とは、有限でない数ですし、有限とは無限大（∞）ではない数としか云えません。つまり、循環の内に開放系を定義することは不可能だと考えます。孤立系をどれだけ拡張しても開放系にならないというのが管理人の出した結論です。
空間とは何か、あるいは「空間の外」とは何かを定義できていない以上、循環である言語で拡張しても表現しきれないのではないかと思うのです。「空間の外とは何か」という疑問そのものをうっちゃれば問題を避けられるように思います。それが「 外のない内 」ということです。その上で空間に関する疑問を別の次元軸に原因を求めようというのが弧理論の考え方です。ですから、弧理論は図１の輪郭内のことを別の次元軸を元に考えることになります。うまく表現できたか甚だ疑問ですが、おわかりいただけるでしょうか？
Follow me!
