昔から流体力学と量子論はつながらない、断絶していると感じていました。弧理論での理解では、微少な領域において空間は曲がっているはずと考察してきました。
注)この記事は読みにくいですが、多くのヒントがあります。
- 2017年12月4日 宇宙という入れ物が膨張しているのではなく「空間が曲がっている」
- 2023年9月27日 自然は映像 小さな領域において、量子力学と全く異なる 物理学 が存在する
空間 の曲がりの結果として、物は運動せざるを得ない(渦)と結論しています。その仕組みの説明は難しいです。(発散トーラスと実体の関係)
- 2024年7月26日 宇宙 は斥力による

ただし、上の記事に示したのは、小さな領域においての観測の結果は離散的、かつ確率的であるが、マクロにおいては連続的に現れる(映像)だということです。

このマクロとミクロの間にある不連続を世の研究者は、どう考えているかを調べてみたら、次の記事がありました。
- academist Hournal『マクロな「流れ」とミクロな「量子」の関係 – 曲がった空間の幾何学を用いて「流れ」を理解する』
この記事では、流体力学と重力理論の類似性に気づいて、「流れ」を幾何学の効果として理解すると言います。
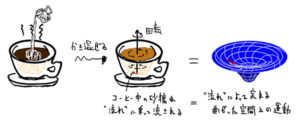
図1 出展:上記リンクより
この考え方の延長上に「量子論に基づいて物質の熱的性質を記述する」ことが研究の目的だと言います。あくまで、ミクロ(量子論)の上にマクロ(流体:熱的性質)があるとの考え方です。
ここで、重力は一般相対性理論により記述されています。これまでに指摘したとおり、相対性理論は循環理論でした。
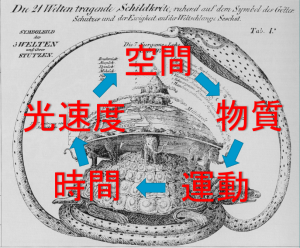
図2
- 物質の運動→時間→光速度(不変の法則?)→時間と空間(物質)
物質の運動から時間を作ります。次に時間を光速度に置き換えます。そして時間 空間 としています。しかし、物質は 空間 内にありますので、全体は循環です。
一般相対性理論は、光速度を空間に対して不変のモノサシとして、一定の結果(空間・質量・重力の関係)を得ています。図1の右端にある空間の歪みは光速度に対しての歪みです。相対論が認知される過程は政治的であったことが知られています。参考(七つの科学事件ファイル―科学論争の顛末)
- 2023年8月14日 宇宙 はアワ(泡構造)を持つウズ(渦:回転運動)
結局、リンク先の記事の目的(流れを幾何学に置き換える)と仕組みは似ていますが、結果は異なります。弧理論において、統計や確率は、物と事の現れる仕組みによると考えるからです。
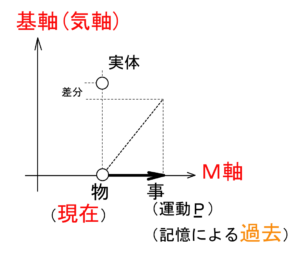
図3 物と事(運動P)は互いに規定し合う繰り返し
もう一つ、academist Hournalには抜け落ちている視点があります。それは、「接するとは何か」です。物と物が接するとは何かです。
ミクロにおいては、離散的確率的に現れますが、マクロにおいては、物質と物質は接しています。これも長年の疑問です。
例を挙げます。電磁誘導は遠隔作用です。
動画1 電磁誘導における作用と反作用
単極モーターにおいて、近接作用と考えられる例です。
動画2
動画3
一連の実験で、接点において力が生じているように見受けられます。
単極モーターにおいて、遠隔作用と考えられる例です。
動画4
明らかに放電を介して力は生じています。ここで、根本的な疑問です。
電磁誘導において、力は引力または斥力ですが、単極誘導の現象においては、接線方向への力、即ち回転運動:渦です。この回転運動にかかる力を卑近ですけれど、「回る」と表現しています。
電磁誘導は「回す」です。往復運動ですから、必ず回転運動に変換する機構が必要です。地球上には、ほぼ「回す」を利用する機器しかありません。
例外的にマグネトロンがありますが、これが科学や産業、技術を複雑にしていますし、効率が悪いです。ご存じの通りマグネトロンは可動部分がありませんし、高効率です。ほぼ故障しません。しかし、これでは資本家は儲かりません。
実は電磁気現象も 空間 の曲がりによって表現できると考えています。その一つの解が発散トーラスです。(発散トーラスで検索)
弧理論による境界空間の模型を示します。


境界面がわかるのは、水と油があるからです。境界面は量的質的にありません。水と油が接しているから渦があり得ます。渦と(引力・斥力)は相対論の(物質と空間の歪み・重力)の関係に似ていますが、異なります。
引力と斥力の例を挙げます。
動画5
実験や模型を参考に「空間の曲がり」について考えてみてください。最後に、弧理論による原子模型を示します。
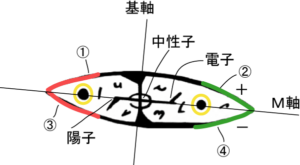
図4 原子の構造は空間の曲がりによる接線方向への斥力という三体問題に帰結する
どうも、紡錘図形の(上弦下弦の)円弧が直線に戻ろうとする作用によって、M軸(物理空間)は凹凸に湾曲するようです。実体が描く円弧の結果、陽子・中性子・電子の周囲の空間は基軸方向に曲がります。これが、M軸に現れる運動(接線方向への斥力:回転運動:渦:回る)であるようです。この説明の過程に発散トーラスが出てきます。
以下のリンクは、発散トーラスの説明です。ただし、↓(弧電磁気論という。)を書いた当時、発散トーラスという名称はありませんでした。図25が発散トーラスの形状を示しています。



