管理人は、” 数学 ができない“と何度か書きました。けれども、考えてみたら代数学ができないのであって、幾何学は出来るのかも知れません。昔、経理をやっていたので、数字が苦手という訳ではありません。しかし、計算が全くできないのです。
研究の成果としての発散トーラスは、幾何学の問題ですので、幾何はできるようです。
図１ 出展：ツカハラ
発散トーラスの発見は、４次元空間でムーンサルト（本家本元ツカハラ）をするような問題で、非常に困難です。調べてみたら、２０１５年５月に初めて発散トーラスという語を使っています。
- 2015年5月6日 これまでの研究と目的
考察をしたのは、２０１１年頃で、内容をまとめて発表したのは、２０１２年１２月２０日でした。以来、発散トーラスの語を含む記事は１１２件あります。
何度も発散トーラスを説明してきましたが、再度、思考過程を書いてみます。
弧理論の骨子は「自然は別の次元軸からの投影による映像だ。」というものです。別の次元軸を基軸と言います。我々のいる自然をＭ軸と言います。あるいは物質的自然、物理空間です。以前は、基軸のことをＥ軸と呼んでいましたが、事情により名称を変更しました。
ある科学者は、電磁気現象を次にように述べています。
- 運動する電子は、周囲に磁場を持つ
電子の運動方向と直交して磁場が出来ますし、磁場の（時間：運動）変化によって、電場ができます。
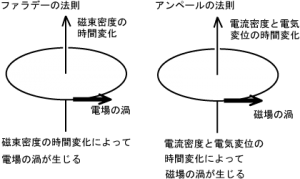
図２ ファラデーの法則 アンペールの法則
これをまとめたのがマクスウェルの方程式です。
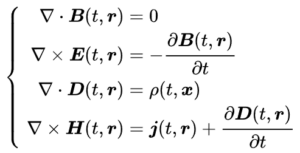
図３
この電気磁気現象を基軸・Ｍ軸間での位相問題として解いて得たのが発散トーラスです。条件は以下です。
図４ トランス（デゴイチ）はコンテナに入っている『フリーエネルギー、UFO、第3起電力で世界は大激変する 永久機関の原理がすでに見つかっていた(超☆わくわく) (超☆わくわく 19) 単行本 2011/10/24』の ｐ２９２より引用
井出治氏が開発した超効率インバーター（デゴイチ）は、特殊な形状をした磁気回路を持つパルストランスです。
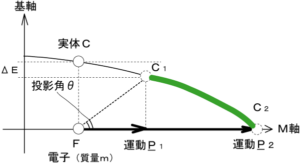
図５
電磁気現象は、電子Ｆと実体Ｃの双対（ダイポール）の位相によると考えます。
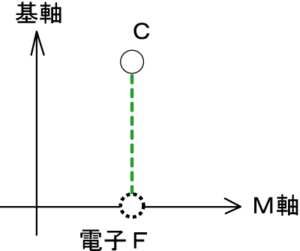図６ 観測者に対して静止した電子（実体Ｃは１２時の位置）
電流は電子の運動です。上図で言えば、投影角θは９０度です。それで、電磁気現象は９０度ごとに起きますので、観測者に対して「１２時の位置（静止状態）～３時の位置、６時の位置、９時の位置」の４つの状態しかありません。
ここで、基軸とＭ軸（ｘ,ｙ,ｚ）間において、位相の変換が起きることによって、運動する電子の周囲に運動方向と直交して磁場が生じると仮定します。
説明は難しいのですが、例えば、Ｃ－Ｆの”対”がＭ軸上ｘ方向に傾斜するとして、ｙ方向に現れます。これは電子の進行方向に直交した磁場です。それで、コイル内にある電子の運動がパルスの場合の磁場の現れる方向と形状を決定したのが発散トーラスです。
ｐ３２に変換の様子を示します。幾つかの変換表と３０枚程度の図表を用いることで、最終的にＭ軸上の形状を決定したのがｐ４９の図２５に示すレンズ状の力場です。思考過程はとても複雑で、これを４次元空間（ｘ、ｙ、ｚ、Ｋ）でのムーンサルトに例えました。
当時は、発散トーラスの形状のみの決定で、名称はありませんでした。
最終的に、トランスに印可されたパルスと同方向（正方向）に電子を加速する力が生じるとの結論を得ました。
通常、電子を加速しても光速度まで加速することは不可能ですが、パルスを用いることによって、正の起電力が生じると証明するものです。これが第３起電力の説明になります。
ここで、パルスを印可するとＭ軸上にＦ－Ｃの対が現れます。【図５の（Ｆ－Ｃ２）】 この対は反時計方向に復帰しようとします（図６の状態に戻ろうとする）。すると電子を印可されたパルスの方向へ引く力が働きます。
Ｃ２－Ｆの”対”は基軸上の静止する位置（１２時の位置）に戻ろうとするが故に電子Ｆを正の方向へ加速すると解釈できます。（この理解はかなり困難です。）これが第３起電力の正体です。
それで、２ヶ月くらいで形状を決定して、１ヶ月で２回程度、検算？、確認した記憶があります。都合、３ヶ月くらいは寝食を忘れて没頭しました。 お読みくださる方で興味がありますならば、ｐｄｆを印刷して思考過程を追ってみてください。
因みに実体は全部で６種類あります。
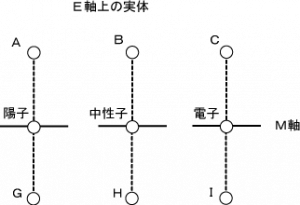
図７ 陽子Ｄ、中性子Ｅ、電子Ｆ（基軸：旧Ｅ軸上に実体は６種）
陽子、中性子、電子のそれぞれに２つの実体があり、その組み合わせによって、差分が磁気双極として現れます。
磁石はＳ極とＮ極の対です。磁石のＳ極やＮ極を単独で取り出すことは決してできません。それは、図３で示されるとおり、空間的に対称だからです。※↓ 弧理論による電磁気学は空間的に非対称です。
弧理論では、発散トーラスという単極の組み合わせによって双極ができます。
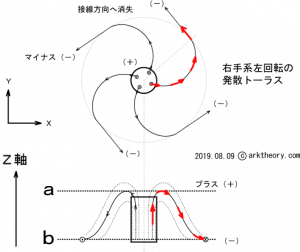
図８ 発散トーラスの形状（双極だが、片方の極ｂに位置は無いため、単極として振る舞う）
発散トーラスには上向き、下向き、右回転、左回転の４種類あります。
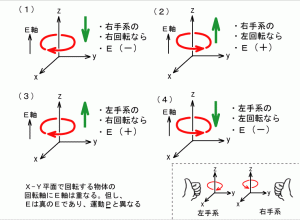
図９ 発散トーラスは４種類ある（Ｅ軸は基軸に読み替えます。）
２つの発散トーラスを組み合わせることで、双極になります。
図１０ 手を使った左回転の模型
例えば、左回転ならば、左手系左回転（＋）の発散トーラスと右手系右回転（－）の発散トーラスを組み合わせた双極になります。弧理論において、磁気双極は、＋－２つの発散トーラスの差分に過ぎません。
井出治氏によるパルストランスは（恐らく）非対称な磁気回路になっていて、通常、打ち消しあうべき差分がわずかに（＋）に大きくなると考えられます。７年くらい前に、井出氏とお会いしましたが、折悪しく図４を拝見することはできませんでした。
以上の説明は、幾何学と考えて良いでしょうか。その意味で 数学（幾何学） ができると言い張ってよいものかどうかです。
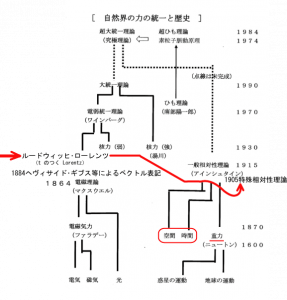
※ 古典電磁気学は成立過程において、非対称な部分を切り捨てたのは、金融資本家による介入があったからです。その経緯は次図です。
図１１ ローレンツによって非対称性は削除された
上記の８．～１０．を参照ください。１８００年代半ばには、ヘヴィサイドによって、回転性電磁気エネルギー流の発見が成されており、これは、非対称性部分を発現する装置であったはずです。これをＪＰモルガンの圧力によって削除されたようです。この非対称性の現象（回転性電磁気エネルギー流）こそ、発散トーラスによったと考えています。次の記事が参考になります。
- 2024年8月9日 アメリカが秘匿してきた「 科学技術 の解禁」
Follow me!
