管理人は２０１２年頃からファラデーの単極誘導について、ネットで調べたり書籍を購入して読んだりした上で、２０１２年末頃より、実験を始めました。 特に参考にしたのは１９８９年発刊のパリティ４巻１２号ｐ８０－８３に掲載された霜田光一氏による「やさしくて難しい電磁気の実験」でした。 動画サイトにはあげてませんけれど、いくつかは実際に確かめました。
その他に参考にしたのはパリティ編集委員会編の「続間違いだらけの物理概念」丸善（株）にある、今井功氏による「磁力線の運動に意味があるか？」（ｐ１２３－１４２）です。 管理人は数学ができませんので、読んでも分かりませんでしたけれど、「磁力線の運動は明確に定義できない」ことや、単極誘導が「磁力線が動くか動かないかはまったく問題外で、要は導体の運動である」と説明されていました。
その他の資料を総合して自分なりに考えてみましたけれど、結局、管理人にはこれらの説明が理解できませんでした。 どこか腑に落ちないのです。 しかしながら、調べた資料のいずれも「単極誘導の起電力は磁力線の密度に比例する」という点は同じでした。たとえば「続間違いだらけの物理概念」では、
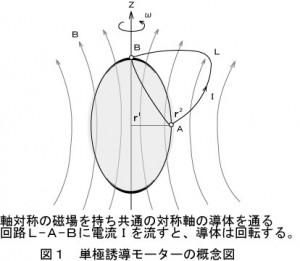
単極誘導は図１のように示されています。（注：同書にある図に管理人がモーターの場合を想定して注釈をつけたものです。） 軸対称の磁場の中で軸対称の導体が共通の対称軸のまわりに回転する場合において、ＡとＢの間に起電力が生じるというもので、閉じた回路Ａ－Ｌ－Ｂには電流が流れるというものです。
図１では一般的な軸対称の回転体について書かれていますけれど、過去記事にあげた電気磁気学の教科書の図ですと次のようになります。
図２
教科書・図２では、回転体は円柱形の磁石を用いて説明しています。 これまでに管理人が調べた上で理解したことを図１と図２を比較ながら考えます。
図１では回転体が卵形ですので、回路Ａ－Ｌ－Ｂの接点Ａが回転体に沿ってＺ軸方向へ移動すると生じる起電力は変化します。理由は、回転体の形が卵形ですので半径が変化するのと同時に回路を貫く磁力線の数が変化するからです。 一方教科書・図２の中の第１１．９図では、接点Ａ１の位置が回転軸Ｚの方向に移動しても、回転体の半径aは変化しません。 また、回路を貫く磁力線の数は「あまり」変化しないと思われます。はっきり断言できる訳ではありませんけれど、一般的には磁石の端面（磁極）や端面の角から多くの磁力線が出入りしているけれど、磁石の側面からはそれほど磁力線の出入りはありません。
ですから、接点Ａ１がＮ極角から遠ざかりＳ極角付近に到達するまでの間は、回路Ａ１－Ｃ１－Ａ２－Ａ３を貫く磁力線の数は、それほど変化しないと判断してよいかと思います。
繰り返しますが、管理人が調べた資料で述べられているのは「単極誘導の起電力は、回転体の角速度ωと半径ｒ（またはa）、磁束密度Ｂに比例する」ということだと理解しています。
マクスウェル方程式から導かれた式１
では、単極誘導において、式１の第１項はゼロですから、第２項を具体的な回転体に置き換えたときに、式１は教科書・図２の式（１１．２４）
Ｕ＝Ｂa^2ω／２ ・・・・・式（１１．２４）
になるということです。 ですから、上記の式が正しいならば教科書・図２において、接点Ａ１がＮ極角から離れて、Ｓ極角付近に到達する間に起電力はそれほど変化しないと考えた訳です。
言い換えると、式の通りだとすると、起電力は Ｎ極付近 ≒ 磁石中央 ≒ Ｓ極付近 であり、一般的に発電機はモーターにもなるので、教科書・図２のような単極誘導モーターを作れば、モーターに生じる回転トルクは発電機と同様に Ｎ極付近 ≒ 磁石中央 ≒ Ｓ極付近 なると理解できます。
ここまでが（管理人が実験を始めた頃の）前提です。 管理人の理解が他の方の理解と同じかどうかは分かりません。
実際のところ、資料ごとに説明が微妙に異なっています。「続間違いだらけの物理概念」では、起電力は軸対称な回転導体に生じるとありますが、別の資料では回路を構成する線路に生じるというのもありました。
単極誘導モーターで、磁石も一緒に回転しているのでは反作用はどこへ行った？ 磁力線は磁石に固定されている？いや空間に固定されている？ 磁力線は運動するのか運動しないのか？ そもそも回転運動とはいったい何か？ などなど、調べるほどに分からないというのが、大方の人に共通する認識ではないでしょうか。 そもそも単極誘導は一部の専門家にしか理解されていないのでは？ 単純に、なぜこれほどに苦労して解釈しなければならないのか。 もっと素直な理解の仕方があるのではないかというのが、当初からの疑問でした。 調べるうち、やがて実際は、１００年以上前に、意図して放置されたらしいことが分かってきました。
Follow me!
