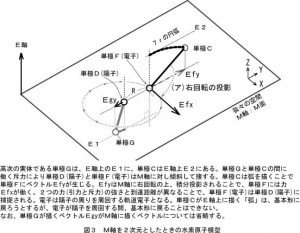
２０１３年２月６日には単極誘導モーターの実験３を行いました。
動画で分かるとおり、プラスの電極は銅円板の中心に取り付けず、銅円板の外縁に取り付けています。この動画の電流の経路は、 電源のプラス側→銅円板の外縁→（接点）細い銅線→電源のマイナス側 へとつながります。 つまり、マクスウェル理論による式１
の示すとおりならば、生じる力は随分小さくなるはずです。なぜなら、電流の経路は磁束密度が比較的小さなところを経由しているからです。
では、電流の経路はネオジム磁石を挟んだ銅板を必ず通らねばならないでしょうか。 そこで単極誘導モーターの実験３－１を行いました。
２０１３年２月６日に行った実験では、右側の銅板を「ネオジム磁石を挟んだ銅板に接触させる」ことで電流を流しています。 動画の実験では、電流は「ネオジム磁石を挟んだ銅円板」を経由していますが、どうも、銅円板を経由しなくても細い銅線（接点）に力は生じるようです。
それで、次に行ったのは単極誘導モーターの実験３－２です。
動画では、ネオジム磁石を挟んだ銅円板を電流は通っていません。つまり、単極誘導モーターに生じる力は「電流の経路に関係なく」かつ「磁石の近傍に接点があればよい」ということになります。
ついでに、動画は作成していませんけれど、このとき確かめたのは、細い銅線の振動はネオジム磁石から「離れることで小さくなる」ということです。 つまり、生じる力は「距離に逆比例する」ということです。
それと、これも動画にしていませんが、右側に置いた銅板を垂直に立てると細い銅線は、垂直に立てた銅板に弾かれるか、立てる方向や電流の向きによっては、銅板に吸着されました。即ち、生じる力は接点の状況がどうあれ、ネオジム磁石の磁極方向と直交した向きに生じるということです。
以上のことを確かめた後で、２０１３年２月１４日に単極誘導モーターの実験２を行いました。
単極誘導モーターに生じる力は、ネオジム磁石の近傍に接点があればよいので、近くにベアリングで支えた銅円板を置けば回転するはずです。この実験で生じる力はかなり弱くて、しかも接点に火花が生じて焼き付くことから何度もビデオの撮り直しをしました。 お気付きのように実験１と実験２は銅円板の回転方向が逆です。当たり前ですけれど。
これまで、実験のことを振り返って、観察したことについて考察するのですが、実験２の回転トルクがなぜ弱いか、考えてみました。
実験２の場合において、式１の右辺の第１項がゼロではないことに気づきました。つまり、右側の銅円板は回転とともにネオジム磁石に近づき、遠ざかるときに磁力線を横切ります。（銅円板にとって、磁束密度が時間的に変化します） つまり、右側の銅円板には電磁誘導による渦電流が生じており、単極誘導モーターにより（接点に）生じる回転トルクを打ち消しているということです。
その後、調べたところによれば、管理人による実験２は、
１８３２年にファラデーが作った単極誘導発電機と同じ形式をモーターにしたものと同じだったと分かりました。ですから、ファラデーが作った発電機も手で回す回転エネルギーの一部は起電力にならなかったことになります。
では、単極誘導モーターに生じる力が「経路に関係ない」のならば、接点を含む回路が磁力線を最も通過させない構造を持つときにも接点に力が生じるかを確かめました。 それが単極誘導モーターの実験４－１です。
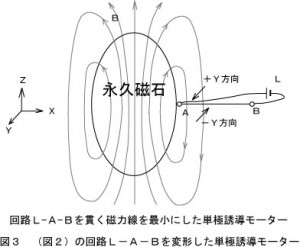
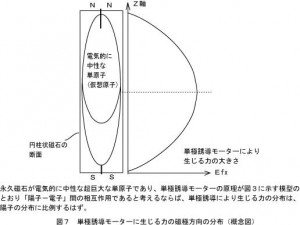
上の動画で、画面右から、電源のプラス→赤い導線→小さな銅片→細いスズメッキ線（接点）→電源のマイナス の順で電流が流れる回路を作ります。 アルニコ磁石の持つ磁力線ができる限り回路を貫かないような経路になっています。模式図で示すと
のようになります。 電源から接点までの経路を磁極方向から眺めると直線上に配置しました。模式図でいうと磁力線の方向がＺ軸方向ですから回路Ｌ－Ａ－ＢをＸ軸上に配置したということです。生じる力は＋Ｙ方向と－Ｙ方向になりますので、接点Ａにある銅片を固定するとスズメッキ線は－Ｙ方向に力を受けることになります。
実験の結果、アルニコ磁石が接点の近傍にあるときは接点に力が生じ、弾かれること、アルニコ磁石遠ざけると力が生じないことを確かめました。これを確認したのが２０１３年５月２１日でした。動画は別途撮影したものです。
一方、実験４－１を行う前の段階で、いろいろな実験の観察により「接点の位置が磁極方向（Ｚ軸方向）の各位置にあるとき」「生じる力が変化する」ことに気づいていました。
接点が磁極方向の各位置で生じる力はどのように分布するかを調べたのが、２０１３年３月２５日に行った単極誘導モーターの実験７です。
ある所で手に入れた水銀を用いて行った実験です。ＤＣ０．６Ｖから０．７Ｖで最大電流６０Ａ～７０Ａというものです。Ｎ極あるいはＳ極付近において、接点の近くで水銀が盛り上がるのが観察できます。この盛り上がりは水銀中を流れる電流が生じる磁力にネオジム磁石の磁力線が作用して水銀の流路が曲げられたものだと考えられます。 そして、水銀貯めに生じた渦が、単極誘導モーターの実験２の銅円板の回転と同じものだと考えられます。 つまり、水銀に生じた渦はネオジム磁石の中央部分が強いのです。 実験７の結果は観察（目視）によるもので、数値化する必要を感じました。
ここで、時系列とは離れますが、磁場中にある電流は力を受けますので、この様子を撮影したものを動画サイトにあげました。 高圧放電の様子 実験４－３です。 ２０１３年１２月ころです。
この実験は、ネオントランスで生じるパルス波を整流した上で、アルニコ磁石の近くで放電させるというものです。ご覧のように、磁極の付近では放電電流が進路を曲げられますけれど、磁石の中央部付近では放電はほぼ直線です。
ところで、単極誘導モーターに生じる力は接点に生じる訳で、スズメッキ線が弾かれる変位の量は、バネの原理から接点に生じる力に比例します。 そこで、単極誘導モーターの実験４を行いました。 実験４は単独で動画サイトにあげていませんので、まとめた動画 「単極誘導モーターに生じる力の解析」の中に収録しました。
実験４は接点の焼き付きをできるだけ押さえて、すべての測定ポイントにおいて安定した値を得るためにかなり苦労しました。実験は２０１３年６月２１日から７月１日で、データ取得と撮影は同時進行でした。
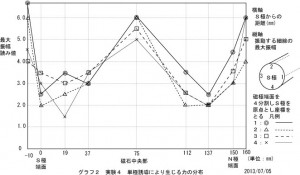
測定は、磁極方向Ｓ極付近からＮ極付近にかけて９カ所について、４回計測しました。接点を安定するために電圧と最大電流・使用するスズメッキ線の太さと支える支点までの長さについて、幾度も予備実験を行いました。 その結果、一部データの不揃いはあるものの、ある程度の傾向は分かる次のグラフ２が得られました。
グラフ２
Ｎ極及びＳ極の両端において、振幅が大きいのは式１の右辺第１項の部分のようです。この場合は回路に力が生じているので、スズメッキ線が撓んでいます。 一方で中央部分での振動、つまり、単極誘導モーターに生じる力によっての振動はスズメッキ線を撓ませていません。この様子を示したのが、単極誘導モーターの実験４－２です。
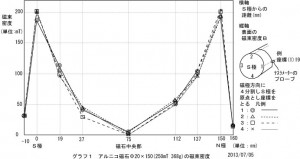
因みに、実験に用いたアルニコ磁石の磁極方向の磁束密度はグラフ１の通りです。
グラフ１
グラフ１は、磁束密度をテスラメーターで測ったのですけれど、テスラメーターはＳ極の値をマイナス表示します。グラフ１は絶対値をグラフにしたものです。 磁石の中央部分の磁束密度はほぼゼロです。単極誘導の起電力が式１の右辺第２項に従うとして、単極誘導モーターに置き換えた場合は、単極誘導モーターに生じる力は磁石中央ではゼロになるはずなのでしょうか？分かりません。 結果は、グラフ２のようにＷの形状をしています。磁極両端の振幅は式１の右辺第１項と考えるとしても、中央部の振幅はどのように理解したらよいのでしょうか？ リンク先（詳しい解説）と「弧電磁気論による中性子を含まない原子模型とファラデーの単極誘導について」を参照下さい。
これら実験を重ねる内に気づいたことがあります。火花放電が起きないときに、スズメッキ線が大きく弾かれるということです。このことはエーテルエンジンの装置に見られた特徴に共通するものがあります。 過去記事か右のブログロールのリンク先（詳しい解説など）を参照下さい。
続いて、単極誘導モーターに生じる力は、磁石の最大磁束密度（いわゆる、磁極端面の磁束密度：カタログ値）に比例すると考えられますが、リンク先にある「弧電磁気論による中性子を含まない原子模型とファラデーの単極誘導について」によれば、どうも磁石の質量に比例すると考えられます。そこで、実験４で用いた装置を使って、大きさの異なる３種類の円柱状磁石に生じる力を比較したのが単極誘導モーターの実験６です。 動画は上記の「単極誘導モーターに生じる力の解析」に含まれています。
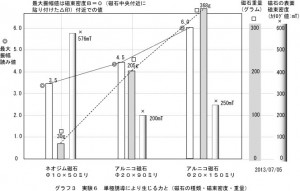
左が長さ５センチのネオジム磁石です。中央が直径２センチ長さ９センチのアルニコ磁石、右が直径２センチ長さ１５センチのアルニコ磁石です。 ３種類の磁石のそれぞれ中央部分での弾かれる最大振れ幅を記録したのがグラフ３です。
グラフ３
用いたネオジム磁石（小）はカタログ値で５７６ｍＴであるのに、最大振れ幅は３．５でした。一方のアルニコ磁石（大）はカタログ値２５０ｍＴで、磁石（小）の２分の１の磁束密度なのに、最大振れ幅は６．０でした。 勿論のこと円柱状の金属が永久磁石でなければ弾かれることはありませんので、磁束密度に比例することは理解できますが、むしろ重さに比例していると見る方が妥当です。
このことについては、過去、記事にしていません。考えられることを記しますと、磁石は
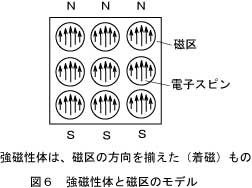小さな結晶の集まりで、これを磁区といい小さな磁石の働きをします。この磁区がバラバラの方向を向いていると、巨視的には磁力を持ちません。磁区が図のように同じ向きをしていれば磁石になります。磁区の方向のそろい方によって磁石の強さが決まるわけです。 ですから、ネオジム磁石は磁区の方向が綺麗にそろっているから磁石として強いということです。
ここで、弧理論の原子模型は次のようなものです。 分かりにくいですけれど
簡単に言えば、図の弧理論による原子模型はファラデーの単極誘導によく似ているということです。 一方で、弧理論の考え方によれば物質の原子が一定の方向にそろっていると巨視的には、超巨大な単原子が存在することに等しいと考えられます。（次図）
すると、上二つの図を勘案して、単極誘導の現象は、「単極誘導の性質は質量に比例する」 が 「磁石の磁区の向きが不揃いになると、超巨大な単原子としての性質が消える」 ということになります。
つまりは、単極誘導モーターに生じる力の強さは、質量に比例するが、単原子としての性質が無くなると消失するはずということです。おそらくは磁力が弱まると単極誘導モーターとして生じる力が弱くなると同時に、中央部のピークが低くなると予想します。要するに分布の曲線が台形に近づくだろうということです。
以上を考慮しながらグラフ３を見るとより理解が深まると思います。 ネオジム磁石は磁石としての性質は強いが、重さが足りないことから単極誘導モーターとして生じる力は小さい。 アルニコ磁石（大）は磁石としての磁区の揃い方が比較的小さい（不揃い）だけれど、元の質量が大きいので単極誘導モーターとして大きな力が生じていると解せます。ですから、「同じ材質」で「重さの異なる」「相似形の」磁石を用いて比較する実験をすれば質量に比例するはずだと考えます。
ここまでの実験結果をまとめたものが以下です。 ファラデーの単極誘導モーターに生じる力は
- 磁力線あるいは磁束密度とは関係がない。
- 接点あるいは接触する面に生じる。
- 電流の経路には関係がない。
- 磁石との距離に逆比例する。
- 磁石の中央部分、重心付近が最も強い。
- 磁石の質量に比例する傾向にある。
- 火花放電が起きないときの方が強い。
ということです。
その後、いろいろ分かりやすい実験を考えたのですけれど、機構的な問題が解決できたので、２０１４年２月２２日から３月１０日にかけて行ったのが単極誘導モーターの実験８です。
まとめの実験ですから、結果は最初から分かっていましたので問題はありませんでした。
以上の結論を書きますと、「ファラデーの単極誘導の現象はだれも理解していなかった」ようです。
なお、「弧理論による中性子を含まない原子模型」は、不十分な内容を含みますことを予めご承知下さい。 （分からないことがありまして、思案中です。）
Follow me!
