人は手指の本数である５の倍数１０を基本とする数学システム（１０進法）を使っています。 管理人はこれまで、弧理論のサイトや当ブログに弧理論の複素数空間はゼータ関数に似ていると書いてきました。ある程度関連性は理解できたのですが、どうも１０進法の数学は３次元物理空間に馴染まないことが分かってきました。 つまり、素数といえば暗黙の内に１０進法の素数を指しますけれど、宇宙の現象と１０進法の素数とは直接の関係がないということです。 角度と素数について理解を深めたいのですが、前段として空間の角度と進数についての考察です。
我々は３次元空間に存在していますが、２次元でも同じですので、いまは２次元平面を等しく分割する場合を考えます。
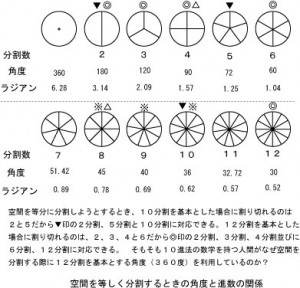図は円を等しく分割したものです。最大１２分割までを図示し、それぞれに分割数、角度とラジアンを書き入れました。
１０分割を基本とした場合を考えます。 １０は２と５で割り切れるので、▼印に示した２分割と５分割、それと１０分割に対応することができます。 また、△印をつけた４分割（２の２倍）と８分割（２の４倍）にも対応ができます。 次に１２分割を基本とした場合では、１２は２と３と４と６で割り切れるので、◎印に示した２分割、３分割、４分割と６分割及び１２分割に対応できます。 また、※印を付けた８分割（２の４倍）と９分割（３の３倍）、それと１０分割（２の５倍）に対応できます。つまり、空間を等しく分割するには、１０を基本とした分割より、１２を基本とした分割の方が多くの場合に対応できるということです。
ですから、素数の性質が宇宙の現象と何らかの関係があるとしても、１０進法による素数は対応する現象と適合する場合が少なく、１２進法による素数の方が宇宙の現象に適合する場合の方がより多いだろうということです。
これまでの所、物理現象は整数であることと物理現象は２πより３６０度に馴染むことは分かってきました。また、上記のように角度に１２進法を用いた方が有用らしいことが分かりました。 上記の表と
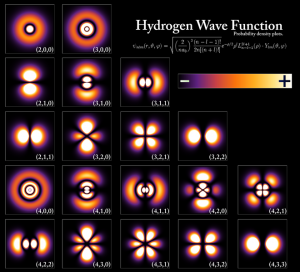
水素の波動関数や
雪の結晶を見比べれば１２を基本とした分割の方がより自然に馴染むことが理解できると思います。 また、方位（方角）・角度から派生して季節（年月）と時刻が１２を基礎にした体系ができたのは当然のことと思います。
ところで、１０進法の数学システムを使用する人間が空間を等しく分割する際に１２分割を基本とする角度（３６０度）を利用しているのはなぜなのでしょうか。いつから？誰が始めたのでしょうか？ １ダースが１２というのはいつからでしょうか？ いつも引用する、ある科学者の言うように１２進法の数学システムを用いるべきだという意見は尤もだと思います。 （管理人は「１２進法による素数列をゼータ関数に適用することによって原子のエネルギー準位を旨く説明できるだろう」と予想しています。どなたか取り組んで頂けたら有り難いです。）
Follow me!
