管理人はこれまで何度か弧理論のサイトと当ブログに次のように書いてきました。
１．時間が問題である。 数学者岡潔の「自然科学者は、時間を決めるときに運動を使う。運動は時間に比例して起こると決めてかかって、そういう時間があると思っている。」という主張から、「運動は時間より求め、時間は運動より求めている」ので究極的には時間を決定していない。
２．従って時間[T]を含む物理量は使えない。
一方で、ある科学者の言葉から次のように書いてきました。
あ） 運動は相対的である。
い） 運動の相対性からエネルギーも相対的な物理量である。
ところで、
う） エネルギーEの次元は、[M][L^2][T^-2] である
ことは物理学として常識であるとともに、（あ）も直観的に正しいことは疑いようがありません。 ということは、（い）の主張が正しいかどうかが問題になります。
観測者の立ち位置によって、質量ｍの物体は運動しているか、静止しているかが決まりますので、（運動の相対性） 観測者Aには対象となる物体が運動しているのでエネルギーを持っていますが、物体とともに移動している観測者Bには対象となる物体が静止しているのでエネルギーを持っていないということになります。（エネルギーの相対性） ですから（い）について、管理人には至極真っ当なことのように感じます。詳しくは右ブログロールリンク先を参照下さい。
（注：ここで、エネルギーには様々な形態があることは承知しています。しかし、運動に関するエネルギーが相対的であるという例外を一つ示せば他の形態のエネルギーについても再考すべきことは、ご理解頂けると思います。）
（あ）を認めるとともに（う）を認めている人が、（い）に納得するならば、自己矛盾になります。（あ）と（う）を認めている人も自己矛盾に気づいていない。 その原因が１．であり２．であるということです。つまり、（う）が誤りであるということです。 但し、この考察において「静止エネルギーがある」という回答は使えません。E=mc^2の光速度cの次元は[L][T^-1]で時間を含むからです。
（い）を認めるならば、①開放系においてエネルギーの総量が保存しているとは言えなくなりますし、②孤立系ではエネルギーの総量は保存していて、①と②の両方が併存することも当然のことになります。 ですから、自然科学は②の孤立系にのみ適用できるのではないかと考えています。 それが数学者岡潔の主張である「五感でわかること」と重なると思います。
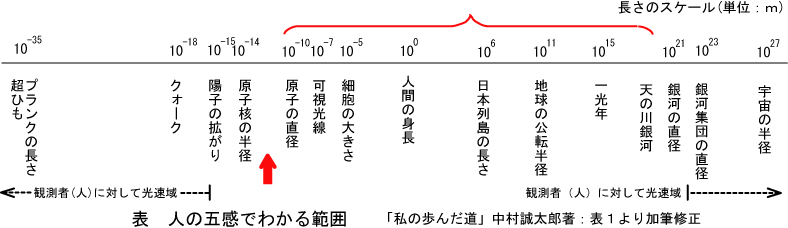
表の赤い括弧で括った範囲が五感でわかる範囲であり、この範囲しか孤立系のシステムである自然科学は適用できないということです。 右端の極大の世界も左端の極微の世界も開放系の力学でしか対応できないと考えます。その候補の一つが弧理論です。
弧理論においては、運動について、ニュートン力学の運動エネルギーK、運動量Pと区別するため運動Pと表記しています。 但し、現時点においては、次元に時間を含まない運動Pは未だ決定していません。
上図の式で可変長の半径Lは消去できますので、恐らく
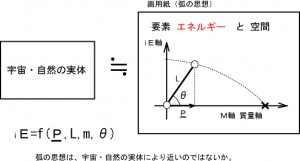
iE=f(P,ｍ,θ)
の関係から導かれると予想しています。ここでエネルギーの真値をE、物体の質量をｍ、E軸上の実体とM軸上の物体との位相をθとします。
このように、エネルギーの問題を時間に置き換えるという極めて簡単で巧妙なすり替えを１９世紀の時点で誰かが意図的にやったと考えていますけれど、確かな証拠はありません。
Follow me!
