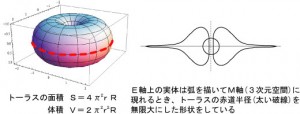
これまで、弧理論の考え方を用いることで超効率インバーター「デゴイチ」の理論的説明を試みました。 その結果、印加したパルスの頂点が持つ(躍度jerk)に応じて、「距離の7乗に逆比例する力場」が生じるらしいことが分かりました。
そして、この力場の3次元形状は、電流により生じる磁場と同じ方向に進み、90度捻る格好でコイル上の電子を加速する方向に無限遠に消失するレンズ状をしているらしいことが分かりました。(図1右) しかしながら、この考察によって、なぜ超効率になるのかを説明出来ませんでした。
また、「弧理論による中性子を含まない原子模型」からファラデーの単極誘導モーターの性質の一端が説明ができるとともに実験により検証することができました。(過去記事や右ブログロール弧理論のサイトを参照下さい)
その後の考察により、弧理論の考え方によって、フリーエネルギー装置実現のヒントとなるアイディアを得ましたので、ここに記します。 ただし、 この考察は、比喩的な話しであり、すぐに実現するものではないことを予めお断りします。
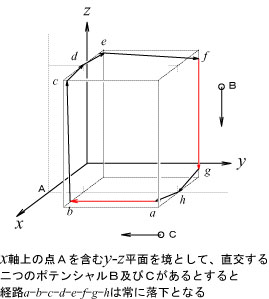
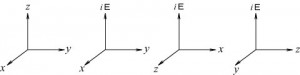
まず、図のように任意の3次元空間に2つの直交するポテンシャルが存在するとします。
X軸上の点Aを含むyz平面を境として、原点の側には-Z方向に引力が存在することとします。これをBとします。 点Aより画面手前側には-Y方向に引力が存在するとします。これをCとします。 ここでAとCは90度方向がずれている訳です。 そして、2つの直交するポテンシャルはyz面において断裂しているものとします。つまり、yz面は不連続面ということです。
いま、不連続面を横断する形で物体がaを出てb→c→d→e→f→g→hの経路をとおりaに戻ることを考えます。すると経路のすべては2つのポテンシャルから引力を受ける落下運動の状態にあることが分かります。特に経路 a→b間、及び f→g間において大きな落差があります。装置の摩擦抵抗を考慮しても連続して運動が生じることになります。
まるで、錯視絵で知られるマウリッツ・エッシャーのWaterfall(滝)と同じです。
しかし、実際に図2のような構造の装置を作っても動作しません。 何故なら、点Aを含むyz面で不連続なポテンシャルを実現することができないからです。 ポテンシャルBは画面手前側Cの領域まで影響を与えるし、ポテンシャルCは原点の側Bの領域まで影響を与えます。 例えば2組の磁石を直交して配置した装置を考案したとして、aからb→c→d→e→f→g→hを経てaへと戻る間の運動エネルギーと位置エネルギーの総和は一定です。摩擦等のロスを入れればマイナスになることは明白です。
動画サイトには永久磁石を使った様々なフリーエネルギー装置があります。中には非常によくできた装置もありますけれど、隠された他の動作原理がなければ永久磁石のみでは不可能ではないかと考えています。
では、上記の「直交する2つのポテンシャル」について、弧理論の考え方ではどうでしょうか。
M軸に直交するE軸上の実体がM軸に現れることで物理現象となるということです。 E軸上の実体はM軸へ「回転を伴う積分投影」されることによって物理現象があらわれる。 また「M軸からE軸へも回転を伴う積分投影」が起きるということです。右ブログロールの「第3起電力のエネルギー源について(考察)」を参照下さい。
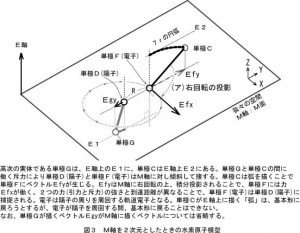
そして、弧理論による中性子を含まない原子模型では
3次元物理空間においては陽子と電子の電荷による引力と、E軸上の実体である単極Gと単極Cの斥力の2つのポテンシャルが存在することによって、水素原子が構成されているというものでした。 図1における2つのポテンシャルは「直交する引力と引力」で、かつ直線運動でしたけれど、図3では「直交する引力と斥力」で、かつ回転運動です。 図1と図3の違いは「E軸とM軸の間の2つのポテンシャルは不連続である」ということです。 この仕組みは現在のところ仮説に過ぎませんけれど、少なくともファラデーの単極誘導モーターの現象は説明できたモデルではあります。 もう一つ大事なことは3次元物理空間は、常にE軸に直交しているということです。 4次元は次図のように4つの3次元空間に分けることが出来ます。
XYZのいずれの回転軸を持つ物体であっても、常にE軸に直交している訳です。 巨視的な地球や葉巻型の宇宙船などは一軸でなければなりませんけれど、原子などはその限りにありません。
現在のところは弧理論によるフリーエネルギー装置の原案はありませんけれど、弧理論の考え方を用いることによって、実験装置からおそらく回転運動としてエネルギーを取り出せると考えています。 当たり前のことですが、弧理論によれば、原子はフリーエネルギー装置そのものだということです。
追記
現代の物理学は理論的に次元軸が11だとうまく説明が出来るとして、次元軸を増やしているのだと思います。 11もある次元軸の間の相互に影響しあうことの想定はしていないのではないかと思います。 超対称性や超超対称性を求めるために次元軸を際限なく増やすことに意味を見いだせません。
西洋の庭園に見られる対称性より、
日本庭園の方が美しいと感じるのは日本人だからでしょうか。
また、非対称な盆栽がなぜ美しいのでしょうか。
ブログランキングの応援と広告のクリックをお願いします。